Активно съпротивление и индуктор в AC веригата

Като се има предвид AC верига, съдържаща само индуктивно съпротивление (вижте статията «Индуктор във верига на променлив ток»), приехме, че активното съпротивление на тази верига е нула.

В действителност, както проводникът на самата бобина, така и свързващите проводници имат макар и малко, но активно съпротивление, така че веригата неизбежно консумира енергията на източника на ток.

Следователно при определяне на общото съпротивление на външна верига е необходимо да се добавят нейните реактивни и активни съпротивления. Но е невъзможно да се добавят тези две различни по природа съпротивления.

В този случай импедансът на веригата към променливия ток се установява чрез геометрично събиране.

Изгражда се правоъгълен триъгълник (виж фигура 1), едната страна на която е стойността на индуктивното съпротивление, а другата страна е стойността на активното съпротивление. Желаният импеданс на веригата се определя от третата страна на триъгълника.

Фигура 1. Определяне на импеданса на верига, съдържаща индуктивно и активно съпротивление

Импедансът на веригата е обозначен с латинската буква Z и се измерва в ома. От конструкцията се вижда, че общото съпротивление винаги е по -голямо от индуктивното и активното съпротивление, взети поотделно.

Алгебричният израз за общото съпротивление на веригата е:

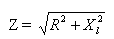
където Z — обща съпротива, R — активно съпротивление, XL — индуктивно съпротивление на веригата.

Поради това, общото съпротивление на веригата към променлив ток, състоящо се от активно и индуктивно съпротивление, е равно на квадратния корен от сумата от квадратите на активното и индуктивното съпротивление на тази верига.

Законът на Ом тъй като такава верига се изразява с формулата I = U / Z,където Z е общото съпротивление на веригата.

Нека сега анализираме какво ще бъде напрежението, ако веригата, в допълнение към и и фазовото изместване между тока и индуктивността, също има относително голямо активно съпротивление. На практика такава верига може да бъде например верига, съдържаща индуктор с желязна сърцевина, навит от тънка жица (високочестотен дросел).

В този случай фазовото изместване между ток и напрежение вече няма да бъде четвърт от периода (както беше във верига само с индуктивно съпротивление), а много по -малко; и колкото по -голямо е съпротивлението, толкова по -малко ще се получи фазовото изместване.

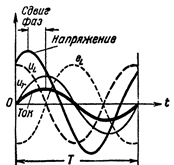
Фигура 2. Ток и напрежение във верига, съдържаща R и Л.

Сега тя самата ЕМП на самоиндукция не е в антифаза с напрежението на източника на ток, тъй като се измества спрямо напрежението не с половината период, а по -малко. В допълнение, напрежението, създадено от източника на ток в клемите на бобината, не е равно на ЕРС на самоиндукция, но е по-голямо от него с размера на спада на напрежението в активното съпротивление на проводника на бобината. С други думи, напрежението в намотката се състои така или иначе от два компонента:

• тиL- реактивният компонент на напрежението, който балансира ефекта на ЕМП от самоиндукция,

• тиR- активният компонент на напрежението, който ще преодолее активното съпротивление на веригата.

Ако свържем последователно голямо активно съпротивление с намотката, фазовото изместване ще намалее толкова много, че текущата синусоида почти ще навакса синусоидата на напрежението и разликата във фазите между тях едва ще се забележи.В този случай амплитудата на термина и ще бъде по -голяма от амплитудата на термина.

По същия начин можете да намалите фазовото изместване и дори напълно да го намалите до нула, ако намалите по някакъв начин честотата на генератора. Намаляването на честотата ще доведе до намаляване на ЕМП на самоиндукция и следователно до намаляване на фазовото изместване между тока и напрежението във веригата, причинено от него.

Силата на AC верига, съдържаща индуктор

Веригата с променлив ток, съдържаща намотката, не консумира енергията на източника на ток и че във веригата има процес на обмен на енергия между генератора и веригата.

Нека сега анализираме как ще стоят нещата със консумираната от такава схема мощност.

Консумираната мощност във веригата на променлив ток е равна на произведението на ток и напрежение, но тъй като токът и напрежението са променливи величини, тогава мощността също ще бъде променлива. В този случай можем да определим стойността на мощността за всеки момент във времето, ако умножим стойността на тока по стойността на напрежението, съответстваща на даден момент във времето.

За да получим графика на мощността, трябва да умножим стойностите на праволинейните сегменти, които определят тока и напрежението в различно време. Такава конструкция е показана на фиг. 3, а. Пунктираната вълнообразна крива p ни показва как мощността се променя във верига на променлив ток, съдържаща само индуктивно съпротивление.

При конструирането на тази крива беше използвано следното алгебрично правило за умножение: Когато положителна стойност се умножи по отрицателна стойност, се получава отрицателна стойност, а когато се умножат две отрицателни или две положителни стойности, се получава положителна стойност.

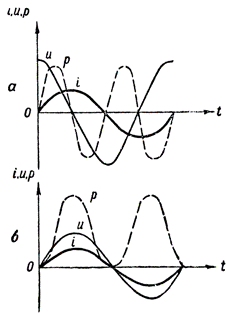
Фигура 3. Графики на мощността: a — във верига, съдържаща индуктивно съпротивление, b — също, активно съпротивление

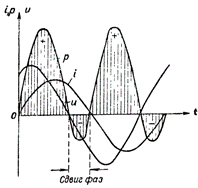
Фигура 4. Графика на мощността за верига, съдържаща R и Л.

Кривата на мощността в този случай се намира над оста на времето. Това означава, че няма обмен на енергия между генератора и веригата и следователно мощността, доставена от генератора към веригата, се консумира напълно от веригата.

На фиг. 4 показва графика на мощността за верига, съдържаща както индуктивно, така и активно съпротивление. В този случай се случва и обратното прехвърляне на енергия от веригата към източника на ток, но в много по -малка степен, отколкото във верига с едно индуктивно съпротивление.

След като прегледаме горните графики на мощността, заключаваме, че само фазовото изместване между ток и напрежение във веригата създава «отрицателна» мощност. В този случай, колкото по -голямо е фазовото изместване между тока и напрежението във веригата, толкова по -малко енергия ще се консумира от веригата и обратно, колкото по -малко е фазовото изместване, толкова по -голяма е мощността, консумирана от веригата.

Прочетете също: Какво е резонанс на напрежението