Логически устройства

За да се опишат законите на функциониране на цифровите схеми, се използва логическа алгебра или булева алгебра. Алгебрата на логиката се основава на концепцията за «събитие», което може или не може да се случи. Събитието, което се е случило, се счита за вярно и изразено логическо ниво «1», събитие, което не е настъпило, се счита за невярно и е изразено логическо ниво «0».

Събитието се влияе от променливи и те влияят според определен закон. Този закон се нарича логическа функцияа променливите са аргументи… Че. логическата функция е функцията y = f (x1, x2, … xn), която приема стойностите «0» или «1». Променливите x1, x2, … xn също имат стойности «0» или «1».

Алгебра на логиката — раздел от математическата логика, който изучава структурата на сложните логически твърдения и начините за установяване на тяхната истина чрез алгебрични методи. Във формулите на логическата алгебра променливите са логически или двоични, тоест те приемат само две стойности- false и true, които се означават съответно с 0 и 1. Всяка компютърна програма съдържа логически операции.

Извикват се устройства, предназначени да образуват функции на логическата алгебра логически устройства… Логическото устройство има произволен брой входове и само един изход (фиг. 1).

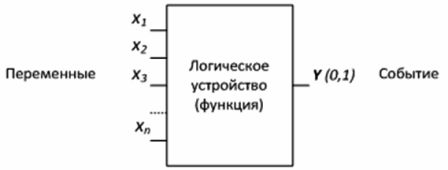
Фигура 1 — Логическо устройство

Например, електронно комбинирано заключване включва логическо устройство, за което събитие (y) е отварянето на ключалката. За да се случи събитието (y = 1), т.е. ключалката се е отворила, е необходимо да се дефинират променливите — десет бутона на клавиатурата с цифри. Трябва да се натиснат определени бутони, т.е. вземете стойността «1» и в същото време натиснете в определена последователност — логическа функция.

Удобно е да представите всяка логическа функция под формата на таблица на състоянието (таблица на истината), където се записват възможни комбинации от променливи (аргументи) и съответната стойност на функцията.

Логическите устройства са изградени върху логически порти, които изпълняват определена функция. Основните логически функции са логическо събиране, логическо умножение и логическо отрицание.

1) ИЛИ (ИЛИ) — логическо добавяне или разделяне (от английски disjunction — прекъсване) — логическа единица се появява на изхода на този елемент, когато единица се появи поне на един от входовете. Изходът ще бъде логическа нула само когато има сигнал за логическа нула на всички входове.

Тази операция може да се осъществи с помощта на контактна верига с два контакта, свързани паралелно. «1» на изхода на такава верига ще се появи, ако поне един от контактите е затворен.

2) И (И) — логическо умножение или свързване (от английския съюз — connection, & — амперсанд) — на изхода на този елемент сигналът на логическа единица се появява само когато логическа единица присъства на всички входове. Ако поне един вход е нула, тогава изходът също ще бъде нула.

Тази операция може да се осъществи чрез контактна верига, състояща се от последователно свързани контакти.

3) НЕ — логическо отрицание или инверсия, обозначен с тире над променлива — операцията се извършва върху една променлива x и стойността на y е противоположна на тази променлива.

Операцията НЕ може да се извърши с помощта на нормално затворен контакт на електромагнитното реле: няма напрежение върху бобината на релето (x = 0) — контактът също е затворен на изхода «1» (y = 1). При наличие на напрежение върху бобината на релето (x = 1), контактът е отворен и на изхода «0» (y = 0).

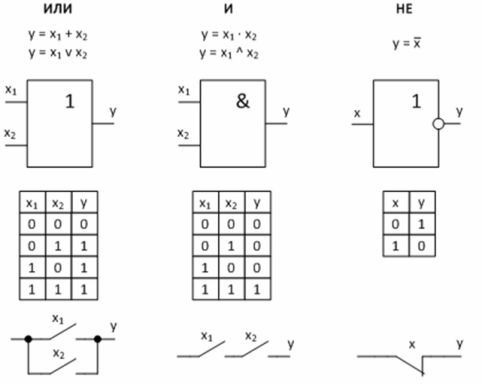
Фигура 2 — Основни логически функции и тяхното изпълнение

Логическите устройства използват различни логически порти. Особено важни са две универсални логически операции, всяка от които е способна независимо да формира всяка логическа функция.

4) NAND — функция на Шефер.

5) ИЛИ НЕ — Функция за пробиване.

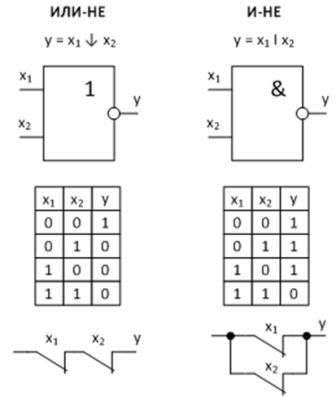
Фигура 3 — Универсални логически функции и тяхното изпълнение

Пример: Алармена верига за сигурност, базирана на логически елементи. Генератор G генерира сигнал на сирена, подавайки го към усилвателния етап чрез логическия елемент «И» на микросхемата DD2. Когато защитните ключове S1 — S4 са затворени, нивото «0» действа на входовете на елемента DD1 — нивото «0» е на долния вход на елемента «I» DD2, което означава, че портата на транзистора VT също е «0».

В случай на отваряне на поне един от ключовете, например S1, входът на елемента DD1 през резистора R1 ще получи напрежение от ниво «1», което ще доведе до появата на «1» на втория вход на елемента «И» DD1. Това ще позволи на сигнала от генератора G да премине към портата на транзистора, чийто товар е високоговорителят.

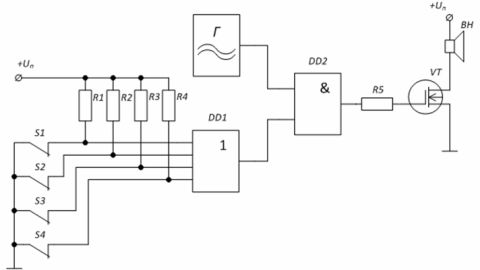
Фигура 4 — Схема за алармена защита

Сложните цифрови схеми се изграждат чрез повтаряне на основни логически схеми отново и отново. Инструментът за такава конструкция е булева алгебра, която по отношение на цифровата технология се нарича алгебра на логиката. За разлика от променлива в обикновената алгебра, булева променлива има само две стойности, които се наричат ​​булева нула и булева една.

Логическата нула и логическата единица се означават с 0 и 1. В логическата алгебра 0 и 1 не са числа, а логически променливи. В логическата алгебра има три основни операции между логическите променливи: логическо умножение (конюнкция), логическо събиране (дизъюнкция) и логическо отрицание (инверсия).

Електронни схеми, изпълняващи същата логическа функция, но сглобени различни елементи, различни по консумация на енергия, захранващо напрежение, стойности на високи и ниски нива на изходно напрежение, време на забавяне на разпространението на сигнала и товароносимост.

Вижте също по тази тема: Логически порти И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и техните таблици на истината