AC кондензатор

Нека сглобим веригата с кондензатор, при който алтернаторът генерира синусоидално напрежение. Нека анализираме последователно какво ще се случи във веригата, когато затворим ключа. Ще разгледаме началния момент, когато напрежението на генератора е равно на нула.

През първото тримесечие на периода напрежението на клемите на генератора ще се увеличи, започвайки от нула и кондензаторът ще започне да се зарежда. Ток ще се появи във веригата, обаче, в първия момент на зареждане на кондензатора, въпреки факта, че напрежението на неговите плочи току -що се е появило и все още е много малко, токът във веригата (зарядният ток) ще бъде най -голям. С увеличаването на заряда на кондензатора токът във веригата намалява и достига нула в момента, когато кондензаторът е напълно зареден. В този случай напрежението върху плочите на кондензатора, стриктно следвайки напрежението на генератора, става в този момент максимално, но с обратен знак, тоест насочено е към напрежението на генератора.

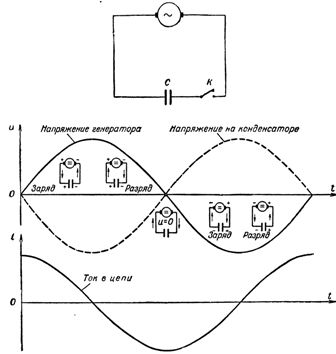
Ориз. 1. Промяна на тока и напрежението във верига с капацитет

По този начин токът се втурва с най -голяма сила в кондензатор безплатно, но веднага започва да намалява, когато плочите на кондензатора се пълнят с заряди и падат до нула, като го зареждат напълно.

Нека сравним това явление с това, което се случва с потока вода в тръба, свързваща два комуникационни съда (фиг. 2), единият от които е пълен, а другият празен. Човек трябва само да натисне клапата, блокираща пътя на водата, тъй като водата веднага от левия съд под голям натиск се втурва през тръбата в празния десен съд. Незабавно обаче налягането на водата в тръбата ще започне постепенно да отслабва поради изравняването на нивата в съдовете и ще падне до нула. Водният поток ще спре.

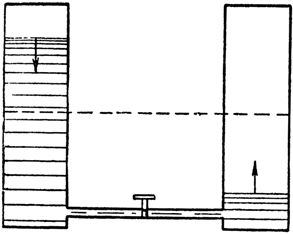
Ориз. 2. Промяната в налягането на водата в тръбата, свързваща комуникационните съдове, е подобна на промяната на тока във веригата по време на зареждането на кондензатора

По същия начин токът първо се втурва в незареден кондензатор, а след това постепенно отслабва, когато се зарежда.

С началото на второто тримесечие на периода, когато първоначално напрежението на генератора стартира бавно, а след това намалява все по -бързо, зареденият кондензатор ще се разрежда към генератора, което ще предизвика разряден ток във веригата. С намаляването на напрежението на генератора кондензаторът се разрежда все повече и разрядният ток във веригата се увеличава. Посоката на разрядния ток през това тримесечие на периода е противоположна на посоката на тока на заряда през първото тримесечие на периода. Съответно кривата на тока, преминала нулевата стойност, сега се намира под оста на времето.

До края на първия полупериод напрежението на генератора, както и на кондензатора, бързо се доближава до нула и токът във веригата бавно достига максималната си стойност. Като се има предвид, че стойността на тока във веригата е колкото по -голяма, толкова по -голяма е стойността на заряда, пренасян по веригата, ще стане ясно защо токът достига своя максимум, когато напрежението върху плочите на кондензатора, и следователно зарядът на кондензатор, бързо намалява.

С началото на третото тримесечие на периода кондензаторът започва да се зарежда отново, но полярността на неговите пластини, както и полярността на генератора се променят „и обратното, а токът, продължаващ да тече в същия посока, започва да намалява с зареждането на кондензатора.В края на третото тримесечие на периода, когато напреженията в генератора и кондензатора достигнат своя максимум, токът отива до нула.

През последната четвърт на периода напрежението, намалявайки, пада до нула и токът, след като е променил посоката си във веригата, достига максималната си стойност. Тук завършва периодът, след което започва следващият, точно повтарящ предишния и т.н.

Така, под действието на променливото напрежение на генератора, кондензаторът се зарежда два пъти през периода (първата и третата четвърт на периода) и два пъти неговото разреждане (втората и четвъртата четвърт от периода). Но тъй като се редуват един по един заряди и разреждания на кондензатора придружен всеки път от преминаване на зареждащия и разреждащия ток през веригата, тогава можем да заключим, че променлив ток.

Можете да проверите това в следния прост експеримент. Свържете 4-6 микрофарад кондензатор към електрическата мрежа чрез 25 W електрическа крушка. Светлината ще светне и няма да изгасне, докато веригата не се прекъсне. Това предполага, че променлив ток е преминал през веригата с капацитета. Разбира се, той преминава не през диелектрика на кондензатора, а във всеки момент от време представлява или ток на заряд, или ток на разреждане на кондензатор.

Както знаем, диелектрикът е поляризиран под действието на електрическо поле, възникващо в него при зареждане на кондензатора, а поляризацията му изчезва при разреждане на кондензатора.

В този случай диелектрикът с възникващия в него ток на изместване служи за променливия ток като своеобразно продължение на веригата, а за константата прекъсва веригата. Но изместващият ток се формира само в рамките на диелектрика на кондензатора и следователно прехвърлянето на заряди по веригата не се случва.

Съпротивлението, предлагано от кондензатор на променлив ток, зависи от стойността на капацитета на кондензатора и от честотата на тока.

Колкото по -голям е капацитетът на кондензатора, толкова по -голям е зарядът по веригата по време на зареждане и разреждане на кондензатора и съответно по -голям ток във веригата. Увеличаването на тока във веригата показва, че съпротивлението му е намаляло.

Следователно, с увеличаване на капацитета, съпротивлението на веригата към променлив ток намалява.

Нараства текуща честота увеличава количеството заряд, пренасяно по веригата, тъй като зарядът (както и разреждането) на кондензатора трябва да се случи по -бързо, отколкото при ниска честота. В същото време увеличаването на размера на прехвърления заряд за единица време е еквивалентно на увеличаване на тока във веригата и следователно на намаляване на неговото съпротивление.

Ако по някакъв начин постепенно намалим честотата на променливия ток и намалим тока до постоянен, тогава съпротивлението на кондензатора, включен във веригата, постепенно ще се увеличи и ще стане безкрайно голямо (прекъсване на веригата), докато се появи в постоянна токова верига.

Следователно, с увеличаване на честотата съпротивлението на кондензатора към променлив ток намалява.

Точно както съпротивлението на намотката към променлив ток се нарича индуктивно, съпротивлението на кондензатор се нарича капацитивно.

Поради това, капацитивното съпротивление е по -голямо, толкова по -нисък е капацитетът на веригата и честотата на тока, който я захранва.

Капацитивното съпротивление се обозначава като Xc и се измерва в ома.

Зависимостта на капацитивното съпротивление от честотата на тока и капацитета на веригата се определя по формулата Xc = 1 /ωС, където ω — кръгова честота, равна на произведението на 2πе, C е капацитетът на веригата във фарад.

Капацитивното съпротивление, подобно на индуктивното, има реактивен характер, тъй като кондензаторът не консумира енергията на източника на ток.

Формула Законът на Ом за верига с капацитет има формата I = U / Xc, където I и U — ефективни стойности на ток и напрежение; Xc е капацитивното съпротивление на веригата.

Свойството на кондензаторите да осигуряват голяма устойчивост на нискочестотни токове и лесно да преминават високочестотни токове се използва широко в схемите на комуникационното оборудване.

С помощта на кондензатори например се постига отделяне на постоянни токове и нискочестотни токове от високочестотни токове, необходими за работата на веригите.

Ако е необходимо да се блокира пътя на нискочестотен ток във високочестотната част на веригата, малък кондензатор е свързан последователно. Той предлага голяма устойчивост на нискочестотен ток и в същото време лесно преминава високочестотен ток.

Ако е необходимо да се предотврати високочестотен ток, например, в захранващата верига на радиостанцията, тогава се използва кондензатор с голям капацитет, свързан паралелно с източника на ток. В този случай високочестотният ток преминава през кондензатора, заобикаляйки захранващата верига на радиостанцията.

Активно съпротивление и кондензатор в AC веригата

На практика често се наблюдават случаи, когато в последователна верига с капацитет е включена активна съпротива. Общото съпротивление на веригата в този случай се определя от формулата

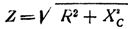
Следователно, общото съпротивление на верига, състоящо се от активно и капацитивно съпротивление на променлив ток, е равно на квадратния корен от сумата от квадратите на активното и капацитивно съпротивление на тази верига.

Законът на Ом остава валиден и за тази верига I = U / Z.

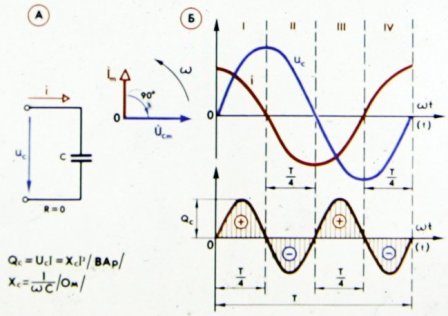
На фиг. 3 показва кривите, характеризиращи фазовата връзка между ток и напрежение във верига, съдържаща капацитивно и активно съпротивление.

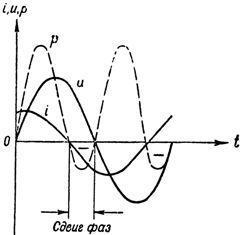
Ориз. 3. Ток, напрежение и мощност във верига с кондензатор и активно съпротивление

Както може да се види от фигурата, токът в този случай повишава напрежението не с една четвърт от период, а по -малко, тъй като активното съпротивление нарушава чисто капацитивния (реактивен) характер на веригата, както се вижда от намаленото фазово изместване . Сега напрежението на клемите на веригата се определя като сума от два компонента: реактивната компонента на напрежението тив, ще преодолее капацитивното съпротивление на веригата и активната съставка на напрежението, преодолявайки активното си съпротивление.

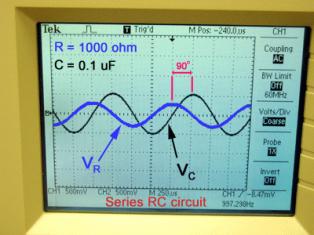
Колкото по -голямо е активното съпротивление на веригата, толкова по -малко е фазовото изместване между ток и напрежение.

Кривата на промяната на мощността във веригата (виж фиг. 3) два пъти през периода придоби отрицателен знак, който, както вече знаем, е следствие от реактивния характер на веригата. Колкото по -малко реактивна е веригата, толкова по -малко е фазовото изместване между ток и напрежение и толкова по -голяма мощност на източника на ток консумира тази верига.

Прочетете също: Напрежение резонанс