Напрежение резонанс

Ако AC веригата е свързана последователно индуктор и кондензатор, тогава те по свой собствен начин влияят на генератора, захранващ веригата, и фазовите връзки между ток и напрежение.

Индукторът въвежда фазово изместване, при което токът изостава от напрежението с една четвърт от период, докато кондензаторът, напротив, прави напрежението във веригата изоставащо от тока с четвърт период. По този начин ефектът на индуктивното съпротивление върху фазовото изместване между ток и напрежение във верига е противоположен на ефекта на капацитивното съпротивление.

Това води до факта, че общото фазово изместване между тока и напрежението във веригата зависи от съотношението на стойностите на индуктивното и капацитивното съпротивление.

Ако стойността на капацитивното съпротивление на веригата е по -голяма от индуктивната, тогава веригата е с капацитивен характер, тоест напрежението изостава от тока във фаза. Ако, напротив, индуктивното съпротивление на веригата е по -голямо от капацитивното, тогава напрежението води тока и следователно веригата е индуктивна.

Общото реактивно съпротивление Xtot на веригата, която разглеждаме, се определя чрез добавяне на индуктивното съпротивление на бобината XL и капацитивното съпротивление на кондензатора XС.

Но тъй като действието на тези съпротивления във веригата е противоположно, тогава на едно от тях, а именно Xc, се присвоява знак минус, а общото реактивно съпротивление се определя по формулата:

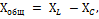
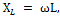
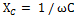
Прилагане към тази верига Законът на Ом, получаваме:

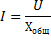
Тази формула може да се трансформира, както следва:

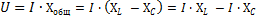
В полученото равенство АзхL —ефективната стойност на компонента на общото напрежение на веригата, която ще преодолее индуктивното съпротивление на веригата, и АзNSС—ефективната стойност на компонента на общото напрежение на веригата, която ще преодолее капацитивното съпротивление.

По този начин общото напрежение на верига, състоящо се от последователно свързване на намотка и кондензатор, може да се разглежда като състоящо се от два члена, чиито стойности зависят от стойностите на индуктивното и капацитивно съпротивление на веригата.

Вярвахме, че такава верига няма активно съпротивление. Въпреки това, в случаите, когато активното съпротивление на веригата вече не е толкова малко, че може да се пренебрегне, общото съпротивление на веригата се определя по следната формула:

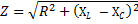
където R е общото активно съпротивление на веригата, XL -NSС — неговата обща реактивност. Преминавайки към формулата на закона на Ом, имаме право да напишем:

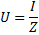
Резонанс на променливотоково напрежение

Индуктивните и капацитивните съпротивления, свързани последователно, причиняват по -малко фазово изместване между ток и напрежение в променливотоковата верига, отколкото ако са включени в схемата отделно.

С други думи, от едновременното действие на тези две реакции с различно естество във веригата, възниква компенсация (взаимно разрушаване) на фазовото изместване.

Пълна компенсация, т.е. пълно премахване на фазовото изместване между ток и напрежение в такава верига, ще настъпи, когато индуктивното съпротивление е равно на капацитивното съпротивление на веригата, т.е.когато XL = XС или, което е същото, когато ωL = 1 / ωС.

В този случай веригата ще се държи като чисто активно съпротивление, тоест сякаш няма нито бобина, нито кондензатор. Стойността на това съпротивление се определя от сумата от активните съпротивления на бобината и свързващите проводници. При което ефективен ток във веригата ще бъде най -големият и се определя от формулата на закона на Ом I = U / Rкъдето Z сега е заменено с R.

В същото време действащите напрежения като на бобината UL = АзхL и на кондензатора Uc = АзNSС ще бъдат равни и ще бъдат възможно най -големи. При ниско активно съпротивление на веригата тези напрежения могат многократно да надвишават общото напрежение U на клемите на веригата. Това интересно явление се нарича в електротехниката резонанс на напрежението.

На фиг. 1 показва кривите на напрежения, ток и мощност при резонанс на напрежения във веригата.

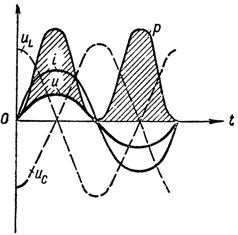
Графика на напрежение ток и мощност при напрежение резонанс

Трябва да се има предвид, че съпротивленията XL техенС са променливи, които зависят от честотата на тока и си струва поне леко да се промени неговата честота, например да се увеличи като XL = ωL ще се увеличи, а XС = = 1 / ωС ще намалее и по този начин резонансът на напрежението във веригата веднага ще бъде нарушен, докато заедно с активното съпротивление, реактивното съпротивление ще се появи във веригата. Същото ще се случи, ако промените стойността на индуктивността или капацитета на веригата.

При резонанс на напрежения, мощността на източника на ток ще се изразходва само за преодоляване на активното съпротивление на веригата, тоест за нагряване на проводниците.

Всъщност, във верига с една индуктивна намотка възникват енергийни колебания, т.е. периодичен пренос на енергия от генератора към магнитно поле бобини. В схема с кондензатор се случва същото, но поради енергията на електрическото поле на кондензатора. Във верига с кондензатор и индуктор при резонанс на напрежението (ХL = XС) енергията, веднъж съхранена от веригата, периодично преминава от бобината към кондензатора и обратно и само консумацията на енергия, необходима за преодоляване на активното съпротивление на веригата, пада на дела на източника на ток. Поради това, обменът на енергия се осъществява между кондензатора и намотката почти без участието на генератора.

Човек трябва само да се счупи резонанс на напрежението по стойност, как енергията на магнитното поле на намотката става неравна на енергията на електрическото поле на кондензатора, а в процеса на обмен на енергия между тези полета ще се появи излишък от енергия, който периодично ще изтича от източника във веригата, след което го върнете обратно към него във веригата.

Това явление е много подобно на това, което се случва в механизма на часовника. Махалото на часовника би могло да се колебае непрекъснато без помощта на пружина (или тежест в часовникарска проходилка), ако не бяха силите на триене, които забавят движението му.

Пружината, като предава част от енергията си на махалото в точния момент, му помага да преодолее силите на триене, като по този начин се постига непрекъснатост на трептенията.

По същия начин в електрическа верига, когато в нея възникне резонанс, източникът на ток изразходва енергията си само за преодоляване на активното съпротивление на веригата, като по този начин подпомага колебателния процес в нея.

Така стигаме до извода, че верига на променлив ток, състояща се от генератор и последователно свързан индуктор и кондензатор, при определени условия XL = XС се превръща в колебателна система… Тази верига беше кръстена колебателна верига.

От равенството XL = XС може да се определи стойностите на честотата на генератора, при които възниква явлението резонанс на напрежението:

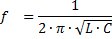
Смисъл капацитет и индуктивност на веригата, при която възниква резонанс на напрежението:

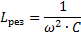
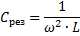
По този начин промяната на някое от тези три количества (еres, L и C), е възможно да се предизвика резонанс на напрежението във веригата, тоест да се превърне веригата в колебателна верига.

Пример за полезно приложение на напрежение резонанс: Входната верига на приемника се настройва от променлив кондензатор (или вариометър) по такъв начин, че в него възниква резонанс на напрежението. Това постига голямо увеличение на напрежението на бобината, необходимо за нормална работа на приемника в сравнение с напрежението във веригата, създадено от антената.

Наред с полезното използване на явлението резонанс на напрежението в електротехниката, често има случаи, когато резонансът на напрежението е вреден.Голямо увеличение на напрежението в отделни секции на веригата (на бобината или на кондензатора) в сравнение с напрежението на генератора може да доведе до повреда на отделни части и измервателни уреди.