Загуби и спадове на напрежението — какви са разликите

В обикновения човешки живот думите „загуба“ и „падане“ се използват за означаване на факта на намаляване на определени постижения, но означават различна стойност.

В този случай «загуби» означава загуба на част, повреда, намаляване на размера на предварително постигнатото ниво. Загубите са нежелателни, но можете да ги търпите.

Думата „падане“ се разбира като по -сериозна вреда, свързана с пълно лишаване от права. По този начин дори понякога възникващи загуби (да речем, портфейл) с течение на времето могат да доведат до спад (например нивото на материалния живот).

В тази връзка ще разгледаме този въпрос във връзка с напрежението на електрическата мрежа.

Как се образуват загуби и падания на напрежението

Електричеството се пренася на дълги разстояния по въздушни линии от една подстанция до друга.

ВЛ са проектирани да предават допустимата мощност и са изработени от метални жила от определен материал и сечение. Те създават резистивен товар със стойност на съпротивление R и реактивен товар X.

На приемащата страна стои трансформаторпреобразуване на електричество. Намотките му имат активно и изразено индуктивно съпротивление XL. Вторичната страна на трансформатора понижава напрежението и го предава по -нататък на потребителите, чието натоварване се изразява със стойността на Z и е с активен, капацитивен и индуктивен характер. Това също влияе върху електрическите параметри на мрежата.

Напрежението, приложено към проводниците на опората на въздушната линия, най -близо до подстанцията за пренос на енергия, преодолява реактивното и активното съпротивление на веригата във всяка фаза и създава ток в нея, чийто вектор се отклонява от вектора на приложеното напрежение с ъгъл φ.

Характерът на разпределението на напреженията и потока от токове по линията за режим на симетрично натоварване е показан на снимката.

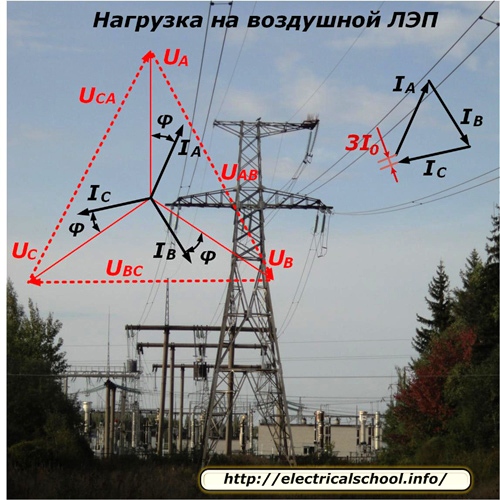
Тъй като всяка фаза на линията захранва различен брой потребители, които също са случайно изключени или свързани към работа, технически е много трудно перфектно да се балансира фазовото натоварване. В него винаги има дисбаланс, който се определя от векторното добавяне на фазовите токове и се записва като 3I0. В повечето изчисления той просто се пренебрегва.

Енергията, изразходвана от предавателната подстанция, се изразходва частично за преодоляване на съпротивлението на линията и достига до приемащата страна с малки промени. Тази фракция се характеризира със загуба и спад на напрежението, чийто вектор намалява леко по амплитуда и се измества под ъгъл във всяка фаза.

Как се изчисляват загубите и спада на напрежението

За да се разберат процесите, протичащи по време на преноса на електричество, е удобна векторната форма за представяне на основните характеристики. Различни математически методи за изчисление също се основават на този метод.

За да се опростят изчисленията в трифазна система той е представен от три еднофазни еквивалентни вериги. Този метод работи добре със симетрично натоварване и ви позволява да анализирате процесите, когато е нарушен.

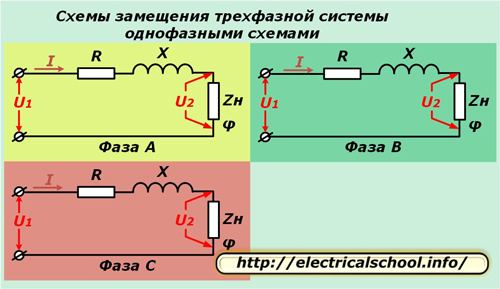
В горните диаграми активният R и реактивното съпротивление X на всеки проводник от линията са свързани последователно със сложното съпротивление на натоварване Zн, характеризиращо се с ъгъла φ.

Освен това се извършва изчисляване на загубата на напрежение и спада на напрежението в една фаза. За да направите това, трябва да посочите данните. За тази цел се избира подстанция, която получава енергия, при която вече трябва да се определи допустимото натоварване.

Стойността на напрежението на всяка система с високо напрежение вече е посочена в справочниците, а съпротивленията на проводниците се определят от тяхната дължина, напречно сечение, материал и конфигурация на мрежата. Максималният ток във веригата е зададен и ограничен от свойствата на проводниците.

Следователно, за да започнем изчисленията, имаме: U2, R, X, Z, I, φ.

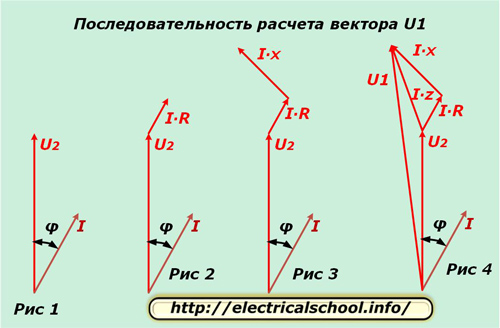
Вземаме една фаза, например, «А» и отделяме за нея в сложната равнина векторите U2 и I, изместени под ъгъл φ, както е показано на фигура 1. Потенциалната разлика в активното съпротивление на проводника съвпада в посока с тока и по величина се определя от израза I ∙ R. Отлагаме този вектор от края на U2 (фиг. 2).

Потенциалната разлика в реактивното съпротивление на проводника се различава от посоката на тока с ъгъл φ1 и се изчислява от продукта I ∙ X. Отлагаме го от вектора I ∙ R (фиг. 3).

Напомняния: за положителната посока на въртене на векторите в сложната равнина се взема движението, противоположно на посоката на часовниковата стрелка. Токът, преминаващ през индуктивния товар, изостава от приложеното напрежение в ъгъл.

Фигура 4 показва начертаването на векторите на потенциалната разлика върху общото съпротивление на проводника I ∙ Z и напрежението на входа на веригата U1.

Сега можете да сравните векторите на входа с еквивалентната верига и при натоварването. За да направите това, поставете получената диаграма хоризонтално (фиг. 5) и изчертайте дъга от началото с радиуса на модула U1, докато се пресече с посоката на вектора U2 (фиг. 6).

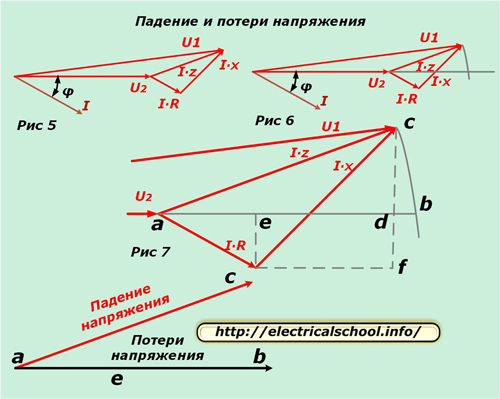
Фигура 7 показва увеличаване на триъгълника за по -голяма яснота и изчертаване на спомагателни линии, обозначаване на характерните точки на пресичане с букви.

В долната част на картината е показано, че полученият вектор ac се нарича спад на напрежението, а ab се нарича загуба. Те се различават по размер и посока. Ако се върнем към първоначалния мащаб, ще видим, че ac се получава в резултат на геометрично изваждане на вектори (U2 от U1), а ab е аритметично. Този процес е показан на снимката по -долу (фиг. 8).

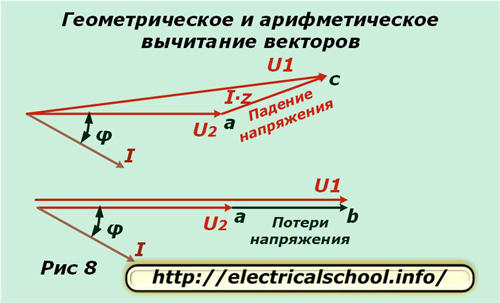
Извеждане на формули за изчисляване на загубите на напрежение

Сега да се върнем на Фигура 7 и да забележим, че bd сегментът е много малък. Поради тази причина тя се пренебрегва в изчисленията и загубата на напрежение се изчислява от дължината на сегмента ad. Състои се от два линейни сегмента ae и ed.

Тъй като ae = I ∙ R ∙ cosφ и ed = I ∙ x ∙ sinφ, тогава загуба на напрежение за една фаза може да се изчисли по формулата:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Ако приемем, че натоварването е симетрично във всички фази (условно пренебрегвайки 3I0), можем да използваме математически методи за изчисляване загуба на напрежение в линията.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Ако дясната страна на тази формула се умножи и раздели на мрежовото напрежение Uн, тогава получаваме формула, която ни позволява да изпълним pИзчисляване на загубите на напрежение чрез захранване.

∆Ul = (P ∙ r + Q ∙ x) / Un

Стойностите на активния P и реактивната Q мощност могат да бъдат взети от показанията на линейните електромери.

По този начин загубата на напрежение в електрическата верига зависи от:

• активно и реактивно съпротивление на веригата;

• компоненти на приложената мощност;

• величината на приложеното напрежение.

Извеждане на формули за изчисляване на напречната компонента на спада на напрежението

Нека се върнем към Фигура 7. Стойността на вектора ac може да бъде представена чрез хипотенузата на правоъгълен триъгълник acd. Вече изчислихме рекламния крак. Нека определим напречната компонента cd.

Фигурата показва, че cd = cf-df.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Използвайки получените модели, ние извършваме малки математически трансформации и получаваме напречната компонента на спада на напрежението.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Определяне на формулата за изчисляване на напрежението U1 в началото на електропровода

Знаейки стойността на напрежението в края на линията U2, загубата ∆Ul и напречната компонента на падането δU, можем да изчислим стойността на вектора U1 по Питагоровата теорема. В разширена форма той има следната форма.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Практическа употреба

Изчисляването на загубите на напрежение се извършва от инженери на етапа на създаване на проект на електрическа верига за оптимален избор на конфигурацията на мрежата и нейните съставни елементи.

По време на експлоатацията на електрически инсталации, ако е необходимо, могат периодично да се извършват едновременни измервания на векторите на напрежението в краищата на линиите и да се сравняват резултатите, получени по метода на прости изчисления.Този метод е подходящ за устройства, които имат повишени изисквания поради необходимостта от висока точност на работа.

Загуби на напрежение във вторични вериги

Пример са вторичните вериги на измервателни трансформатори на напрежение, които понякога достигат няколкостотин метра дължина и се предават от специален захранващ кабел с увеличено напречно сечение.

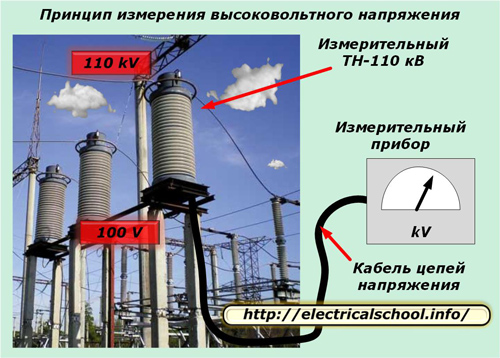
Електрическите характеристики на такъв кабел са предмет на повишени изисквания за качеството на предаване на напрежение.

Съвременната защита на електрическите съоръжения изисква работа на измервателни системи с високи метрологични показатели и клас на точност 0,5 или дори 0,2. Следователно, загубите на подаденото към тях напрежение трябва да бъдат наблюдавани и взети предвид. В противен случай грешката, въведена от тях в работата на оборудването, може значително да повлияе на всички експлоатационни характеристики.

Загуби на напрежение в дълги кабелни линии

Характеристиката на дизайна на дългия кабел е, че той има капацитивно съпротивление поради доста близкото разположение на проводящи жила и тънък слой изолация между тях. Той допълнително отклонява текущия вектор, преминаващ през кабела, и променя неговата величина.

Ефектът от намаляване на напрежението върху капацитивното съпротивление трябва да се вземе предвид при изчислението, за да се промени стойността на I ∙ z. В противен случай описаната по -горе технология не се променя.

Статията предоставя примери за загуби и спадове на напрежението върху въздушни електропроводи и кабели. Те обаче се срещат при всички потребители на електроенергия, включително електрически двигатели, трансформатори, индуктори, кондензаторни банки и други устройства.

Размерът на загубите на напрежение за всеки тип електрическо оборудване е законово регламентиран по отношение на условията на работа, а принципът на тяхното определяне във всички електрически вериги е един и същ.