Трифазно мрежово захранване: активно, реактивно, пълно

Стойностите на общата активна и общата реактивна мощност на трифазната верига са равни съответно на сумите на активната и реактивната мощност за всяка от трите фази A, B и C. Това твърдение е илюстрирано от следните формули:

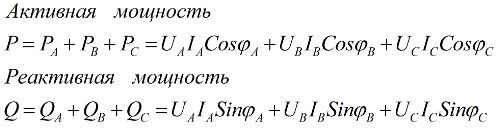
тук Ua, Ub, Uc, Ia, Ib, Ic са стойностите на фазовите напрежения и токове, а φ е фазовото изместване.

Когато натоварването е симетрично, тоест в условия, когато активната и реактивната мощност на всяка от фазите са равни една на друга, за да се намери общата мощност на многофазната верига, е достатъчно да се умножи стойността на фазовата мощност с броя на участващите фази. Общата мощност се определя въз основа на получените стойности на нейните активни и реактивни компоненти:

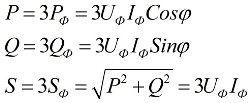
В горните формули фазовите стойности на количествата могат да бъдат изразени чрез техните линейни стойности, които ще се различават за схемите за свързване звезда или триъгълник за потребителите, но формулите за мощността в крайна сметка ще се окажат еднакви:

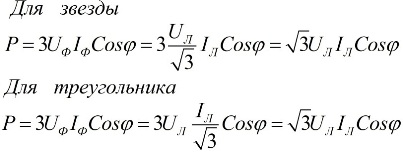
От горните изрази следва, че независимо от схемата на свързване на приемниците на електрическа енергия, независимо дали е триъгълник или звезда, ако натоварването е симетрично, тогава формулите за намиране на мощността ще имат еднаква форма, и двете за триъгълник и за звезда:

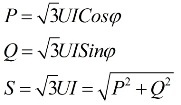
Тези формули показват линейни стойности на напрежение и ток и са написани без индекси. Обикновено се намира такава нотация, без индекси, тоест ако няма индекси, тогава имаме предвид линейни стойности.

За извършване на измервания във връзка с активната мощност в електрическата верига се използва специално измервателно устройство, което се нарича ватметър… Неговите показания се определят по формулата:

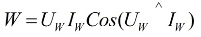
в горната формула, Uw и Iw са векторите на напрежението, приложено към товара, и тока, протичащ през него.

Характерът на активното натоварване и диаграмата на фазовото свързване могат да бъдат различни, следователно, в зависимост от конкретните обстоятелства, схемите за свързване на ватметър ще бъдат различни.

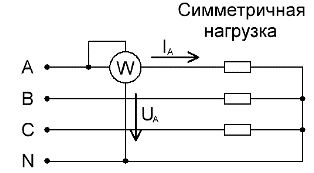
За симетрично натоварени трифазни вериги, за грубо измерване на общата активна мощност, ако не се изисква висока точност, е достатъчен един ватметър, свързан само към една от фазите. След това, за да се получи стойността на активната мощност на цялата верига, остава да се умножат показанията на ватметъра по броя на фазите:

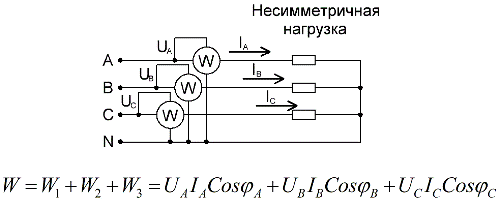
За четирипроводна верига с неутрален проводник, за точно измерване на активната мощност, са необходими три ватметра, всеки от които се отчита и след това се сумира, за да се получи стойност за общата мощност на веригата:

Ако в трифазна верига няма неутрален проводник, тогава два ватметра са достатъчни за измерване на общата мощност, дори ако натоварването е небалансирано.

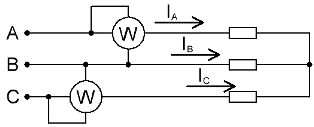
При липса на неутрален проводник фазовите токове са свързани помежду си в съответствие с първия закон на Кирххоф:

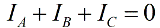
Тогава сумата от показанията на двойка ватметри ще бъде равна на:

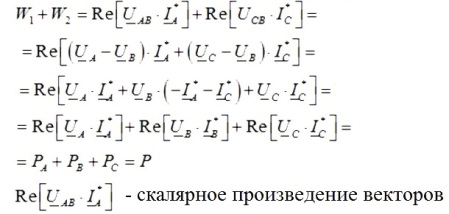
Така че, ако съберете показанията на чифт ватметри, получавате общата активна мощност в изследваната трифазна верига, а показанията на ватметрите ще зависят както от размера на товара, така и от неговия характер.

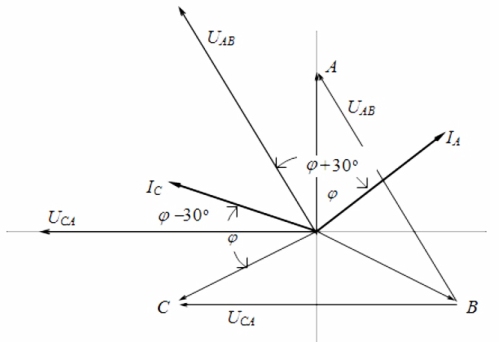
Разглеждайки векторната диаграма на токове и напрежения във връзка със симетрично натоварване, може да се стигне до заключението, че показанията на ватметрите се определят по следните формули:

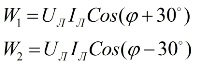
След като анализираме тези изрази, може да се разбере, че при чисто активно натоварване, когато φ = 0, показанията на двата ватметъра ще бъдат равни една на друга, тоест W1 = W2.

При активна индуктивност на товара, когато 0 ≤ φ ≤ 90 °, показанията на ватметър 1 ще бъдат по-малки от тези на ватметър 2, тоест W1 60 °, показанията на ватметър 1 ще бъдат отрицателни , тоест W1 <0.

При активно -капацитивен характер на натоварването, когато 0 ≥ φ≥ -90 °, показанията на ватметъра 2 ще бъдат по -малки от ватметъра 1, тоест W1> W2. При φ <-60 ° показанията на ватметъра 2 ще станат отрицателни.