Измерване на DC и AC еднофазен ток

От израза за мощността при постоянен ток P = IU може да се види, че тя може да бъде измерена с помощта на амперметър и волтметър по непряк метод. В този случай обаче е необходимо да се извърши едновременно отчитане от два инструмента и изчисления, които усложняват измерванията и намаляват неговата точност.

За измерване на мощност в DC и еднофазен променлив ток те използват устройства, наречени ватметри, за които се използват електродинамични и феродинамични измервателни механизми.

Електродинамичните ватметри се произвеждат под формата на преносими устройства с класове на висока точност (0,1 — 0,5) и се използват за точни измервания на AC и DC мощност при индустриални и повишени честоти (до 5000 Hz). Феродинамични ватметри по -често vте се намират под формата на панелни инструменти с относително нисък клас на точност (1.5 — 2,5).

Такива ватметри се използват главно при променлив ток с промишлена честота. При постоянен ток те имат значителна грешка поради хистерезиса на ядрата.

За измерване на мощност при високи честоти се използват термоелектрически и електронни ватметри, които са магнитоелектричен измервателен механизъм, оборудван с активен преобразувател на мощност към постоянен ток. Конверторът на мощност извършва операцията по умножение потребителски интерфейс = p и получаване на сигнал на изхода, който зависи от продукта потребителски интерфейс, тоест от властта.

На фиг. 1, и е показана възможността за използване на електродинамичен измервателен механизъм за конструиране на ватметър и измерване на мощността.

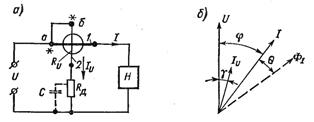
Ориз. 1. Схема за превключване на ватметър (а) и векторна диаграма (б)

Неподвижната бобина 1, свързана последователно към товарната верига, се нарича серийна верига на ватметъра, движещата се бобина 2 (с допълнителен резистор), свързана паралелно с товара — паралелната верига.

За постоянен ватметър:

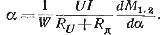
Помислете за работата на електродинамичен ватметър при променлив ток. Векторна диаграма фиг. 1, b е изграден за индуктивния характер на товара. Текущ вектор Iu паралелната верига изостава от вектора U в ъгъла γ поради известна индуктивност на движещата се бобина.

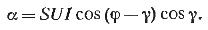
От този израз следва, че ватметърът правилно измерва мощността само в два случая: когато γ = 0 и γ = φ.

Състояние γ = 0 може да се постигне чрез създаване резонанс на напрежението в паралелна верига, например, чрез включване на кондензатор C със съответния капацитет, както е показано с пунктирана линия на фиг. 1, а. Резонансът на напрежението обаче ще бъде само при определена специфична честота. Условие за промяна на честотата γ = 0 е нарушено. При γ не е равно на 0, ватметърът измерва мощността с грешка βy, която се нарича ъглова грешка.

При малка стойност на ъгъла γ (γ обикновено не повече от 40 — 50 ‘), относителна грешка

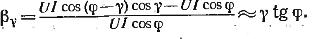
В ъглите φблизо до 90 °, ъгловата грешка може да достигне големи стойности.

Втората, специфична грешка на ватметрите е грешката, причинена от консумацията на енергия на бобините му.

При измерване на консумираната от товара мощност, две вериги за превключване на ватметър, различаващи се по включването на неговата паралелна верига (фиг. 2).

Ориз. 2. Схеми за включване на паралелната намотка на ватметъра

Ако не вземем предвид фазовите отмествания между токовете и напреженията в бобините и считаме натоварването Н за чисто активно, грешките βа) и β(б), поради консумацията на енергия на намотките на ватметъра, за веригите на фиг. 2, a и b:

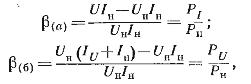
където П.i и П.ти — съответно мощността, консумирана от серийната и паралелната верига на ватметъра.

От формулите за βа) и β(б) може да се види, че грешките могат да имат забележими стойности само при измерване на мощността в схеми с ниска мощност, т.е. когато Pi и П.ти съизмерим с Rn.

Ако промените знака само на един от токовете, посоката на отклонение на движещата се част на ватметъра ще се промени.

Ватметърът има две двойки скоби (серийни и паралелни вериги) и в зависимост от включването им във веригата, посоката на отклонение на показалеца може да бъде различна. За правилното свързване на ватметъра, една от всяка двойка скоби е маркирана с «*» (звездичка) и се нарича «генераторска скоба».