Импулсен ток

В различни електронни устройства, например в оборудване с електронни и полупроводникови устройства, т.е.в усилватели, токоизправители, радиостанции, генератори, телевизори, както и във въглеродни микрофони, телеграфи и много други устройства, те се използват широко пулсационни токове и напрежения… За да не повтаряме разсъжденията два пъти, ще говорим само за токове, но всичко, което е свързано с токове, е вярно и за напреженията.

Пулсиращите токове, които имат постоянна посока, но променят стойността си, могат да бъдат различни. Понякога текущата стойност се променя от най -високата към най -ниската стойност, която не е равна на нула. В други случаи токът се намалява до нула. Ако верига с постоянен ток се прекъсва с определена честота, след това за някои интервали от време няма ток във веригата.

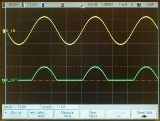
На фиг. 1 показва графики на различни токове на вълни. На фиг. 1, a, b, промяната в токовете настъпва съгласно синусоидална крива, но тези токове не трябва да се считат за синусоидални променливи токове, тъй като посоката (знакът) на тока не се променя. На фиг. 1, в показва ток, състоящ се от отделни импулси, тоест краткотрайни „удари“ на ток, отделени един от друг с паузи с по-голяма или по-малка продължителност и често се нарича импулсен ток. Различните импулсни токове се различават един от друг по формата и продължителността на импулсите, както и по скоростта на повторение.

Удобно е да се разглежда пулсиращ ток от всякакъв вид като сума от два тока — преки и променливи, наречени термини или компоненти, токове. Всеки пулсиращ ток има постоянни и променливи компоненти. Това изглежда странно за мнозина. Всъщност в крайна сметка пулсиращият ток е ток, който тече през цялото време в една посока и променя стойността си.

Как можете да кажете, че съдържа променлив ток, който променя посоката си? Ако обаче два тока — постоянен и променлив — преминават едновременно през един и същ проводник, се оказва, че в този проводник ще тече пулсиращ ток (фиг. 2). В този случай амплитудата на променливия ток не трябва да надвишава стойността на постоянния ток. Постоянните и променливите токове не могат да преминават отделно по проводника. Те добавят към общ поток от електрони, който има всички свойства пулсиращ ток.

Ориз. 1. Графики на различни токове на вълни

Добавянето на AC и DC токове може да бъде показано графично. На фиг. 2 показва графиките на постоянен ток, равен на 15 mA, и променлив ток с амплитуда 10 mA. Ако сумираме стойностите на тези токове за отделни точки във времето, като вземем предвид посоките (знаците) на токовете, получаваме графиката на тока на вълните, показана на фиг. 2 с удебелена линия. Този ток варира от най -ниската стойност от 5 mA до най -високата стойност от 25 mA.

Разгледаното добавяне на токове потвърждава валидността на представянето на пулсиращия ток като сума от постоянни и променливи токове. Правилността на това представяне се потвърждава и от факта, че с помощта на някои устройства е възможно да се отделят компонентите на този ток един от друг.

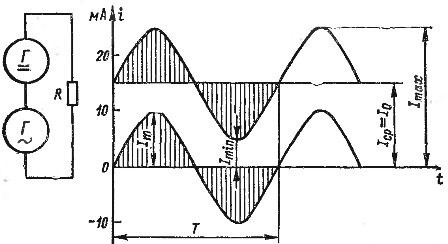
Ориз. 2. Получаване на пулсационен ток чрез добавяне на постоянен и променлив ток.

Трябва да се подчертае, че всеки ток винаги може да бъде представен като сума от няколко тока. Например, ток от 5 А може да се счита за сумата от токове 2 и 3 А, протичащи в една посока, или сумата от токове 8 и 3 А, протичащи в различни посоки, тоест, с други думи, разликата между токовете 8 и 3 А.Не е трудно да се намерят други комбинации от два или повече тока, даващи общо 5 А.

Тук има пълна прилика с принципа на добавяне и разлагане на силите. Ако две еднакво насочени сили действат върху който и да е обект, те могат да бъдат заменени с една обща сила. Силите, действащи в противоположни посоки, могат да бъдат заменени с единична разлика. И обратно, дадена сила винаги може да се счита за сумата от съответните еднакво насочени сили или за разликата между противоположно насочените сили.

Не е необходимо директните или синусоидалните променливи токове да се разлагат на компонентни токове. Ако заменим пулсиращия ток със сумата от постоянни и променливи токове, тогава чрез прилагане на известните закони на постоянни и променливи токове към тези компонентни токове е възможно да се решат много проблеми и да се направят необходимите изчисления, свързани с пулсиращия ток.

Концепцията за пулсиращ ток като сума от постоянни и променливи токове е условна. Разбира се, не може да се предположи, че в определени интервали от време директните и променливите токове наистина текат един към друг по проводника. Всъщност няма два противоположни потока от електрони.

В действителност пулсиращият ток е единичен ток, който променя стойността си с течение на времето. По -правилно е да се каже, че пулсиращото напрежение или пулсиращото ЕМП може да бъде представено като сума от постоянните и променливите компоненти.

Например, на фиг. 2 показва как алгебрично постоянната ЕДС на един генератор се добавя към променливата ЕДС на друг генератор. В резултат на това имаме пулсираща ЕМП, която причинява съответния пулсиращ ток. Условно обаче може да се счита, че постоянният ЕМП създава постоянен ток във веригата, а променливият ЕМП — променлив ток, който, като се сумира, образува пулсиращ ток.

Всеки пулсиращ ток може да се характеризира с максималните и минималните стойности на Itax и Itin, както и неговите постоянни и променливи компоненти. Постоянната компонента се обозначава с I0. Ако променливият компонент е синусоидален ток, тогава неговата амплитуда се обозначава с Iт (всички тези количества са показани на фиг. 2).

Не трябва да се смесва помежду си It и Itax. Също така, максималната стойност на вълната на тока Imax не трябва да се нарича амплитуда. Понятието амплитуда обикновено се отнася само до променливи токове. По отношение на пулсиращия ток можем да говорим само за амплитудата на неговата променлива компонента.

Постоянният компонент на пулсиращия ток може да се нарече средната му стойност Iav, тоест средната аритметична стойност. Всъщност, ако вземем предвид промените в един период на пулсиращия ток, показан на фиг. 2, ясно се вижда следното: през първия полупериод към тока от 15 mA се добавят редица стойности чрез промяна на токовия компонент, вариращ от 0 до 10 mA и отново до 0, а през втория полупериод, точно същите стойности на тока се изваждат от тока 15 mA.

Следователно токът от 15 mA наистина е средната стойност. Тъй като токът е пренасянето на електрически заряди през напречното сечение на проводника, то Iav е стойността на такъв постоянен ток, който в един период (или за цял брой периоди) пренася същото количество електричество като този пулсиращ ток.

За синусоидален променлив ток стойността на Iav за период е нула, тъй като количеството електричество, преминало през напречното сечение на проводника в един полупериод, е равно на количеството електричество, което преминава в обратна посока по време на друг полупериод. На графиките на токове, показващи зависимостта на тока i от времето t, количеството електричество, пренасяно от тока, се изразява с площта на фигурата, ограничена от кривата на тока, тъй като количеството електричество се определя от продукта, който той .

За синусоидален ток областите на положителната и отрицателната полувълна са равни.В пулсиращия ток, показан на фиг. 2, през първия полупериод количеството електричество, пренасяно от компонента на променливия ток, се добавя към количеството електричество, пренасяно от тока Iav (засенчена площ на фигурата). А през втория полуцикъл се изважда точно същото количество електричество. В резултат на това през целия период се прехвърля същото количество електроенергия, както при един постоянен ток Iav, тоест площта на правоъгълника Iav T е равна на площта, ограничена от кривата на тока на вълните.

По този начин постоянният компонент или средната стойност на тока се определя от прехвърлянето на електрически заряди през напречното сечение на проводника.

Уравнението на тока, показано на фиг. 2, очевидно трябва да бъде написано в следната форма:

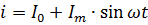
Мощността на пулсиращия ток трябва да се изчисли като сумата от мощностите на съставящите го токове. Например, ако токът, показан на фиг. 2, преминава през резистор с съпротивление R, тогава неговата мощност е

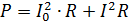
където I = 0,7Im е средноквадратичната стойност на променливия компонент.

Можете да въведете концепцията за ефективната стойност на Id тока на вълната. Мощността се изчислява по обичайния начин:

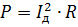
Приравнявайки този израз към предишния и го редуцирайки с R, получаваме:

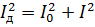
Същите взаимоотношения могат да бъдат получени при напрежения.