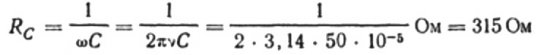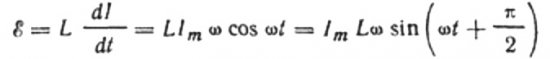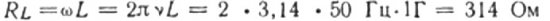Капацитивно и индуктивно съпротивление във верига на променлив ток
Ако включим кондензатор в DC верига, откриваме, че той има безкрайно съпротивление, тъй като постоянен ток просто не може да премине през диелектрика между плочите, тъй като диелектрикът по дефиниция не провежда постоянен електрически ток.
Кондензаторът прекъсва DC веригата. Но ако същият кондензатор сега е включен във веригата на променлив ток, тогава се оказва, че неговият кондензатор не изглежда да се счупи напълно, той просто се редува и зарежда, тоест електрическият заряд се движи, а токът във външната верига се поддържа.
Въз основа на теорията на Максуел в този случай можем да кажем, че променливият ток на проводимост вътре в кондензатора е все още затворен, само в този случай — от тока на отклонение. Това означава, че кондензаторът във веригата на променлив ток действа като вид съпротивление с крайна стойност. Тази съпротива се нарича капацитивен.

Практиката отдавна показва, че количеството променлив ток, протичащ през проводник, зависи от формата на този проводник и от магнитните свойства на средата около него. При прав проводник токът ще бъде най -голям и ако същият проводник се навие в бобина с голям брой завои, токът ще бъде по -малък.
И ако в същата намотка се въведе и феромагнитно ядро, токът ще намалее още повече. Следователно проводникът осигурява променлив ток не само с омично (активно) съпротивление, но и с допълнително съпротивление, в зависимост от индуктивността на проводника.Тази съпротива се нарича индуктивни.
Неговият физически смисъл е, че променящият се ток в проводник с определена индуктивност инициира ЕМП на самоиндукция в този проводник, която има тенденция да предотвратява промени в тока, тоест има тенденция да намалява тока. Това е равносилно на увеличаване на съпротивлението на проводника.
Капацитет в променливотоковата верига
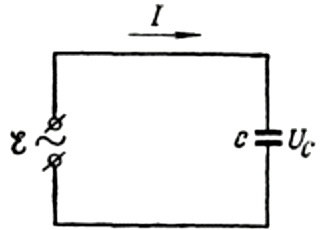
Първо, нека поговорим по -подробно за капацитивното съпротивление. Да предположим, че кондензатор с капацитет С е свързан към синусоидален източник на променлив ток, тогава ЕМП на този източник ще бъде описан със следната формула:
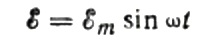
Ще пренебрегнем спада на напрежението върху свързващите проводници, тъй като той обикновено е много малък и ако е необходимо, може да се разгледа отделно. Нека сега да приемем, че напрежението върху плочите на кондензатора е равно на напрежението на източника на променлив ток. Тогава:
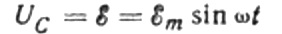
Във всеки един момент зарядът на кондензатор зависи от неговия капацитет и от напрежението между неговите плочи. След това, за даден известен източник, който беше споменат по -горе, получаваме израз за намиране на заряда върху кондензаторните плочи чрез напрежението на източника:
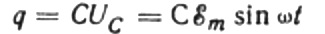
Нека за безкрайно малко време dt зарядът на кондензатора се промени с dq, след това ток I ще тече през проводниците от източника към кондензатора, равен на:
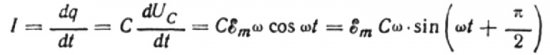
Стойността на амплитудата на тока ще бъде равна на:
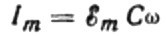
Тогава крайният израз за текущия ще бъде:
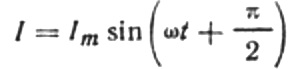
Нека препишем формулата за текущата амплитуда в следния вид:
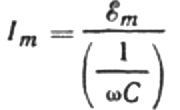
Това съотношение е законът на Ом, където реципрочното на произведението на ъгловата честота и капацитета играе ролята на съпротивление и всъщност е израз за намиране на капацитета на кондензатор в синусоидална верига с променлив ток:
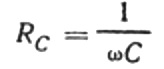
Това означава, че капацитивното съпротивление е обратно пропорционално на ъгловата честота на тока и капацитета на кондензатора. Лесно е да се разбере физическият смисъл на тази зависимост.
Колкото по-голям е капацитетът на кондензатора в променливотоковата верига и колкото по-често се променя посоката на тока в тази верига, в крайна сметка повече общ заряд преминава за единица време през напречното сечение на проводниците, свързващи кондензатора към източника на променлив ток. Това означава, че токът е пропорционален на произведението на капацитета и ъгловата честота.
Например, нека изчислим капацитета на кондензатор с електрически капацитет 10 микрофарада за синусоидална верига с променлив ток с честота 50 Hz:
Ако честотата беше 5000 Hz, тогава същият кондензатор би представлявал съпротивление от около 3 ома.
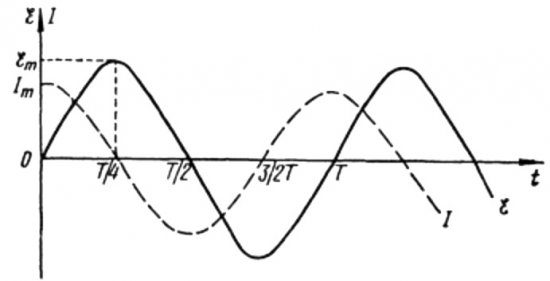
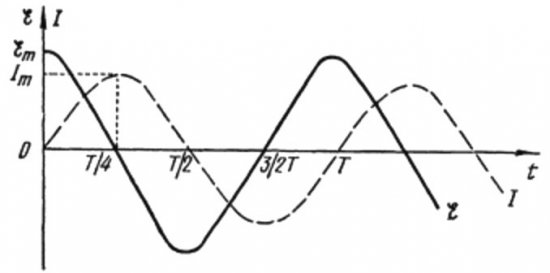
От горните формули става ясно, че токът и напрежението във верига на променлив ток с кондензатор винаги се променят в различни фази. Текущата фаза води фазата на напрежението с pi / 2 (90 градуса). Това означава, че максималният ток във времето винаги съществува четвърт период по -рано от максималното напрежение. По този начин върху капацитивното съпротивление токът изпреварва напрежението с четвърт период от време или с 90 градуса във фаза.
Нека обясним физическия смисъл на това явление. В първия момент от времето кондензаторът се разрежда напълно, така че най -малкото напрежение, приложено към него, вече премества зарядите върху плочите на кондензатора, създавайки ток.
Тъй като кондензаторът се зарежда, напрежението върху неговите плочи се увеличава, това предотвратява по -нататъшния приток на заряд, така че токът във веригата намалява въпреки по -нататъшното увеличаване на напрежението, приложено към плочите.
Това означава, че ако в началния момент от време токът е бил максимален, тогава когато напрежението достигне своя максимум след четвърт период, токът ще спре напълно.
В началото на периода токът е максимален, а напрежението минимално и започва да се увеличава, но след една четвърт от периода напрежението достига максимум, но токът вече е спаднал до нула до този момент. Така се оказва, че напрежението изпреварва напрежението с една четвърт от периода.
AC индуктивно съпротивление
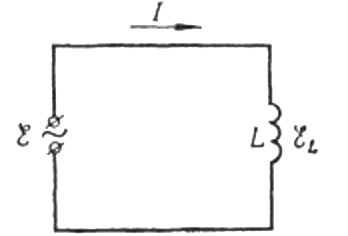
Сега да се върнем към индуктивното съпротивление. Да приемем, че променлив синусоидален ток протича през бобина с индуктивност. Може да се изрази така:
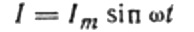
Токът се дължи на променливото напрежение, приложено към бобината. Това означава, че върху намотката ще се появи ЕМП на самоиндукция, която се изразява по следния начин:
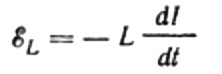
Отново пренебрегваме спада на напрежението върху проводниците, свързващи източника на ЕМП към бобината. Омичното им съпротивление е много ниско.
Нека променливото напрежение, приложено към бобината във всеки момент от времето, да бъде напълно балансирано от възникващата ЕМП на самоиндукция, равна на нея по величина, но противоположна по посока:
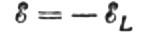
Тогава имаме право да напишем:
Тъй като амплитудата на напрежението, приложено към бобината, е:
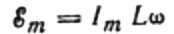
получаваме:
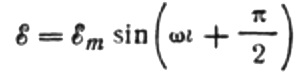
Нека изразим максималния ток, както следва:
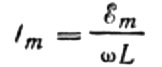
Този израз по същество е законът на Ом. Количество, равно на произведението на индуктивността и ъгловата честота, играе ролята на съпротивление тук и не е нищо повече от индуктивното съпротивление на индуктора:

И така, индуктивното съпротивление е пропорционално на индуктивността на бобината и ъгловата честота на променливия ток през тази намотка.
Това се дължи на факта, че индуктивното съпротивление се дължи на влиянието на ЕМП на самоиндукция върху напрежението на източника,-ЕМП на самоиндукция има тенденция да намалява тока и следователно носи съпротивлението във веригата . Величината на ЕРС на самоиндукция, както е известно, е пропорционална на индуктивността на бобината и скоростта на промяна на тока през нея.
Например, нека изчислим индуктивното съпротивление на бобина с индуктивност 1 H, която е включена във верига с токова честота 50 Hz:
Ако честотата на топката беше 5000 Hz, тогава съпротивлението на същата намотка би било равно на приблизително 31 400 ома.Припомнете си, че омичното съпротивление на проводника на бобината обикновено е няколко ома.
От горните формули е очевидно, че промените в тока през бобината и напрежението в нея се случват в различни фази, а фазата на тока винаги е по -малка от фазата на напрежението при pi / 2. Следователно максималният ток възниква четвърт период по -късно от началото на максималното напрежение.
При индуктивното съпротивление токът изостава от напрежението с 90 градуса поради спирачния ефект на самоиндукционната ЕМП, която предотвратява промяната на тока (и увеличаването и намаляването), поради което максималният ток се наблюдава във веригата с намотката по -късно от максималното напрежение.
Бобина и кондензатор комбинирано действие
Ако свържете бобина с кондензатор последователно с верига на променлив ток, тогава напрежението на бобината ще ускори напрежението на кондензатора във времето с половин период, тоест с 180 градуса във фаза.
Капацитивно и индуктивно съпротивление се наричат реактанти… Енергията не се изразходва в реактивно съпротивление, както в активно съпротивление. Енергията, натрупана в кондензатора, периодично се връща обратно към източника, когато електрическото поле в кондензатора изчезне.
Същото е и с намотката: докато магнитното поле на бобината се създава от тока, енергията в нея се натрупва през една четвърт от периода, а през следващата четвърт от периода се връща към източника. В тази статия говорихме за синусоидален променлив ток, за който тези разпоредби се спазват стриктно.
В синусоидални вериги с променлив ток, индуктори с ядра се наричат задушаватрадиционно се използват за ограничаване на тока. Тяхното предимство пред реостати е, че енергията не се разсейва в огромни количества под формата на топлина.