Непрекъснати колебания и параметричен резонанс
Непрекъснати вибрации — вибрации, чиято енергия не се променя с течение на времето. В реалните физически системи винаги има причини, които причиняват прехода на вибрационната енергия към топлинна енергия (например триене в механични системи, активно съпротивление в електрически системи).
Следователно, незаглушени трептения могат да бъдат получени само при условие, че тези загуби на енергия се попълнят. Подобно попълване се извършва автоматично в автоколебателни системи поради енергия от външен източник. Непрекъснатите електромагнитни трептения се използват изключително широко. За получаването им се използват различни генератори.

За да се направят електрическите или механичните вибрации (на трептящ кръг или махало) незаглушени, е необходимо през цялото време да се компенсират съпротивлението или загубите от триене.
Можете например да действате върху колебателната верига с променлив ЕМП, което периодично ще увеличава тока в бобината и съответно ще поддържа амплитудата на напрежението в кондензатора. Или можете да натиснете махалото по подобен начин, поддържайки хармоничното му люлеене.
Както знаете, величината на енергията на магнитното поле на бобината на трептящата верига е свързана с нейната индуктивност и ток чрез следната връзка (втората формула еенергия на електрическото поле на кондензатора същия контурен контур)
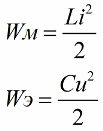
От първата формула става ясно, че ако периодично увеличаваме тока в бобината, действайки по променливата верига на ЕМП, тогава (чрез увеличаване или намаляване на втория фактор във формулата — ток) периодично ще попълваме тази верига с енергия.
Действайки върху веригата строго във времето с нейните естествени свободни трептения, тоест на резонансната честота, ще получим явлението електрически резонанс, защото е на резонансната честота колебателна система най -интензивно абсорбира доставената му енергия.
Но какво ще стане, ако периодично променяте не втория фактор (не тока или напрежението), а първия — индуктивност или капацитет? В този случай веригата също ще претърпи промяна в енергията си.
Например, периодично натискане и излизане на сърцевината от намотката или натискане и излизане от кондензаторадиелектрик, — получаваме и съвсем определена периодична промяна в енергията във веригата.
Пишем тази позиция за единична промяна в индуктивността на бобината:
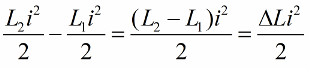
Най -изразителният ефект от люлеенето на веригата ще се окаже, ако промените в индуктивността се извършат точно навреме. Например, ако вземем същата верига в произволен момент във времето, когато през нея вече тече някакъв ток i, и въведем ядро в бобината, тогава енергията ще се промени със следното количество:
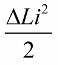
Сега нека се появят свободни трептения в самата верига, но в момента, в който след четвърт период енергията напълно е преминала в кондензатора и токът в бобината се е превърнал в нула, ще извадим рязко сърцевината от бобина Индуктивността ще се върне в първоначалното си състояние, до първоначалната стойност L. Не е необходимо да се харчи работа срещу магнитното поле, когато сърцевината е извадена. Следователно, когато сърцевината беше избутана в намотката, веригата получи енергия, тъй като ние работихме, стойността на която:
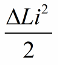
След една четвърт от периода кондензаторът започва да се разрежда, неговата енергия отново се преобразува в енергията на магнитното поле на намотката.Когато магнитното поле достигне амплитуда, отново ще натиснем рязко ядрото. Отново индуктивността се увеличи, увеличена със същото количество.
И отново, при нулев ток, връщаме индуктивността към първоначалната й стойност. В резултат на това, ако енергийните печалби за всеки полупериод надвишават загубите на съпротивление, енергията на контура ще се увеличава през цялото време и амплитудата на трептене ще се увеличава. Тази ситуация се изразява с неравенството:
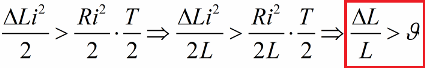
Тук разделихме двете страни на това неравенство с L и записахме условието за възможността за параметрично възбуждане чрез скокове за определена стойност на логаритмичния декремент.
Препоръчително е да променяте индуктивността (или капацитета) два пъти за период, поради което честотата на промяната на параметъра (честотата на параметричния резонанс) трябва да бъде два пъти естествената честота на трептящата система:
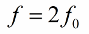
Така че пътят на възбуждане на трептенията във веригата се е появил, без да е необходимо директно да се променя ЕМП или ток. Първоначалният флуктуационен ток във веригата винаги присъства по един или друг начин и това дори не взема предвид смущенията от радиочестотните трептения в атмосферата.
Ако индуктивността (или капацитетът) не се променя в скокове, а хармонично, тогава условието за възникване на трептения ще изглежда малко по -различно:
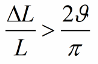
Тъй като капацитетът и индуктивността са параметри на веригата (като масата на махалото или еластичността на пружината), методът на възбуждащи трептения се нарича още параметрично възбуждане.
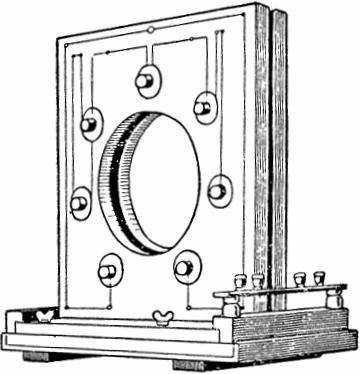
Това явление е открито и изследвано на практика в началото на 20 век от съветските физици Манделщам и Папалекси. Въз основа на това физическо явление те построиха първия параметричен генератор на променлив ток с мощност 4 kW и променлива индуктивност.
В дизайна на генератора седем двойки плоски намотки бяха разположени от двете страни на рамката, в кухината на която се въртеше феромагнитен диск с издатини. Когато дискът се задвижва с въртене от двигател, издатините му периодично влизат и излизат от пространството между всяка двойка намотки, като по този начин се променят индуктивността и вълнуващите трептения.
