Изчисляване на полученото съпротивление при последователно-паралелна връзка

Понятия и формули

Последователно-паралелна или смесена връзка е сложна връзка от три или повече съпротивления. Полученото съпротивление на смесена връзка се изчислява на етапи, като се използват формули за изчисляване на съпротивления в последователни и паралелни връзки.

Примери за

1. Изчислете последователно-паралелната връзка на три съпротивления съгласно диаграмата на фиг. 1.

Първо, заменете паралелно свързаните съпротивления r2 и r3 с полученото съпротивление r (2-3):

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 ома.

Полученото съпротивление на цялата верига е r = r1 + r (2-3) = 5 + 6.6 = 11.6 ома.

Ориз. 1.

2. Какъв ток протича през веригата (фиг. 2) в случаите на отворено и затворено превключвател с нож П? Как се променя напрежението на съпротивлението r2 и в двата случая?

Ориз. 2.

а) Превключвателят е отворен. Резултатно съпротивление на последователно свързани съпротивления r1 и r2

r (1-2) = r1 + r2 = 25 ома.

Ток I (1-2) = U / r (1-2) = 100/25 = 4 A.

Спад на напрежението на съпротивлението r2

U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.

б) Превключвателят е затворен. Резултатно съпротивление на паралелно свързани резистори r1 и r3

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 ома.

Общото съпротивление на цялата верига е r = r (1-3) + r2 = 6,6 + 5 = 11,6 ома.

Ток I = U / r = 100 / 11,6 = 8,62 A.

Падането на напрежението на съпротивлението r2 в този случай е равно на: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.

Във втория случай токът се увеличи в резултат на свързването на паралелното съпротивление R3. Повече ток създава повече спад на волтажа при съпротивление r2.

3. Какво трябва да бъде допълнителна съпротива rd, така че две паралелно свързани лампи за напрежение 120 V и ток 0,2 A могат да бъдат свързани към мрежа с напрежение U = 220 V (фиг. 3)?

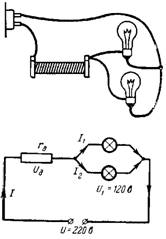
Ориз. 3.

Напрежението в лампите трябва да бъде равно на 120 V. Останалото напрежение (100 V) пада при допълнителното съпротивление rd. Ток на две лампи I = 0,4 A преминава през съпротивлението rd.

Според закона на Ом rd = Ud / I = 100 / 0.4 = 250 Ohm.

4. Електронните лампи с нажежаема жичка 1,2 V и ток на нажежаема жичка 0,025 и 0,05 A са свързани последователно към източник на постоянен ток с напрежение 4,5 V. Какво трябва да бъде допълнителното съпротивление rd и паралелно съпротивление (шунт) към лампа с по -нисък ток на нажежаема жичка (фиг. 4)?

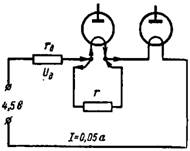
Ориз. 4.

Съпротивленията във веригата трябва да бъдат избрани така, че токът с нажежаема жичка на втората лампа да тече I = 0,05 A. Напрежението върху нажежаемата жичка на електронните лампи ще бъде 1,2 + 1,2 = 2,4 V. Изваждайки тази стойност от напрежението на батерията, ние вземете стойността на спада на напрежението през допълнителното съпротивление rd: Ud = 4.5-2.4 = 2.1 V.

Следователно допълнителното съпротивление rd = (Ud) / I = 2.1 / 0.05 = 42 Ohm.

Токът на нажежаема жичка от 0,05 А не трябва да тече през нишката на първата вакуумна тръба. Половината от този ток (0,05-0,025 = 0,025 А) трябва да премине през шунта r. Напрежението на шунта е същото като на нажежаемата жичка на лампата, т.е. 1,2 V. Следователно, съпротивлението на шунта е: r = 1,2 / 0,025 = 48 Ohm.

5. Какви са полученото съпротивление на веригата и токът в нея във веригата на фиг. 5?

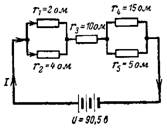
Ориз. 5.

Първо, нека определим полученото съпротивление на паралелно свързаните съпротивления:

r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 ома;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 ома.

Полученото съпротивление на веригата е:

r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 ома.

Резултатният ток при напрежение U = 90,5 V

I = U / r = 90,5 / 15,05 = 6 А.

6. Изчислете полученото съпротивление на сложна последователно-паралелна връзка във веригата на фиг. 6. Изчислете получения ток I, ток I4 и спад на напрежението върху съпротивлението r1.

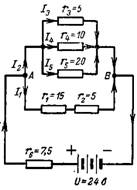
Ориз. 6.

Резултатна проводимост на паралелно свързани съпротивления

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;

r (3-4-5) = 20/7 = 2,85 ома.

Съпротивлението на веригата на r1 и r2 е:

r (1-2) = r1 + r2 = 15 + 5 = 20 ома.

Получената проводимост и съпротивление между точки A и B са съответно равни: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 ома.

Полученото съпротивление на цялата верига е r = rAB + r6 = 2,5 + 7,5 = 10 ома.

Полученият ток е I = U / r = 24/10 = 2,4 A.

Напрежението между точки A и B е равно на напрежението на източника U минус спада на напрежението на съпротивлението r6

UAB = U-I ∙ r6 = 24- (2,4 ∙ 7,5) = 6 V.

Съпротивлението r4 е свързано с това напрежение, така че токът, преминаващ през него, ще бъде равен на:

I4 = UAB / r4 = 6/10 = 0,6 A.

Резисторите r1 и r2 имат общ спад на напрежението UAB, така че токът, преминаващ през r1, е:

I1 = UAB / r (1-2) = 6/20 = 0,3 A.

Спад на напрежението на съпротивление r1

Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.

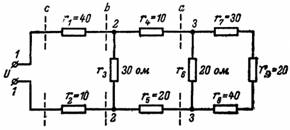
7. Какви са полученото съпротивление и ток във веригата на фиг. 7, ако напрежението на източника е U = 220 V?

Ориз. 7.

Започваме с веригата, разположена вдясно от възли 3 и 3. Съпротивленията r7, r8, r9 са свързани последователно, следователно

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 ома.

Паралелно с това съпротивление е включено съпротивление r6, така че полученото съпротивление в възел 3 и 3 (раздел а)

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 ома.

Съпротивленията r4 и r5 са свързани последователно със съпротивление ra:

r (4-5-a) = 10 + 20 + 16.36 = 46.36 ома.

Резултатно съпротивление на възли 2 и 2 (раздел б)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46.36 ∙ 30) / (46.36 + 30) = 1390.8 / 76, 36 = 18.28 ома.

Полученото съпротивление на цялата верига е r = r1 + rb + r2 = 40 + 18.28 + 10 = 68.28 ома.

Полученият ток е I = U / r = 220 / 68.28 = 3.8 A.