Спад на волтажа

Понятия и формули

При всяко съпротивление r при преминаване на тока I се появява напрежение U = I ∙ r, което обикновено се нарича спад на напрежението на това съпротивление.

Ако има само едно съпротивление r в електрическата верига, цялото напрежение на източника Ust пада върху това съпротивление.

Ако веригата има две съпротивления r1 и r2, свързани последователно, тогава сумата от напреженията в съпротивленията U1 = I ∙ r1 и U2 = I ∙ r2, т.е. спада на напрежението, е равна на напрежението на източника: Ust = U1 + U2.

Напрежението на захранването е равно на сумата от спада на напрежението във веригата (2 -ри закон на Кирххоф).

Примери за

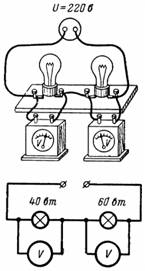
1. Какъв спад на напрежението възниква върху нажежаемата жичка на лампата с съпротивление r = 15 Ohm, когато токът I = 0.3 A премине (фиг. 1)?

Ориз. 1.

Броят на спада на напрежението Законът на Ом: U = I ∙ r = 0,3 ∙ 15 = 4,5 V.

Напрежението между точки 1 и 2 на лампата (вижте диаграмата) е 4,5 V. Лампата свети нормално, ако номиналният ток преминава през нея или ако има номинално напрежение между точки 1 и 2 (номиналният ток и напрежението са посочени на лампа).

2. Две еднакви крушки за напрежение 2,5 V и ток 0,3 A са свързани последователно и са свързани към джобна батерия с напрежение 4,5 V. Какъв спад на напрежението се генерира на клемите на отделните крушки (фиг. 2) )?

Ориз. 2.

Идентичните крушки имат еднакво съпротивление r. Когато са свързани последователно, през тях преминава същият ток I. От това следва, че те ще имат еднакви спадания на напрежението, сумата от тези напрежения трябва да е равна на напрежението на източника U = 4,5 V. Всяка крушка има напрежение 4,5: 2 = 2,25 V.

Можете да решите този проблем и последователно изчисление. Изчисляваме съпротивлението на крушката според данните: rl = 2,5 / 0,3 = 8,33 Ohm.

Ток на веригата I = U / (2rl) = 4,5 / 16,66 = 0,27 A.

Падането на напрежението върху крушката U = Irl = 0,27 ∙ 8,33 = 2,25 V.

3. Напрежението между релсата и контактния проводник на трамвайната линия е 500 V. За осветление се използват четири еднакви лампи, свързани последователно. За какво напрежение трябва да се избере всяка лампа (фиг. 3)?

Ориз. 3.

Идентичните лампи имат равни съпротивления, през които протича един и същ ток. Спадът на напрежението в лампите също ще бъде същият. Това означава, че за всяка лампа ще има 500: 4 = 125 V.

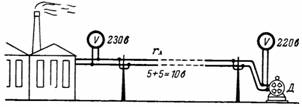
4. Две лампи с мощност 40 и 60 W с номинално напрежение 220 V са свързани последователно и са свързани към мрежа с напрежение 220 V. Какъв спад на напрежението възниква върху всяка от тях (фиг. 4)?

Ориз. 4.

Първата лампа има съпротивление r1 = 1210 Ohm, а втората r2 = 806.6 Ohm (в нагрято състояние). Токът, преминаващ през лампите, е I = U / (r1 + r2) = 220 / 2016.6 = 0.109 A.

Спад на напрежението в първата лампа U1 = I ∙ r1 = 0,109 ∙ 1210 = 132 V.

Спад на напрежението във втората лампа U2 = I ∙ r2 = 0,109 ∙ 806,6 = 88 V.

Лампа с по -високо съпротивление има по -голям спад на напрежението и обратно. Нишките на двете лампи са много слаби, но лампата от 40 W е малко по -силна от лампата от 60 W.

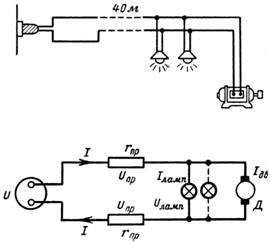
5. За да може напрежението на електродвигателя D (фиг. 5) да бъде равно на 220 V, напрежението в началото на дългата линия (при електроцентралата) трябва да бъде повече от 220 V по стойността спад на напрежението (загуба) на линия. Колкото по -голямо е съпротивлението на линията и токът в нея, толкова по -голям е спадът на напрежението по линията.

Ориз. 5.

В нашия пример спадът на напрежението във всеки проводник на линията е 5 V. Тогава напрежението на шините на електроцентралата трябва да бъде равно на 230 V.

6. Потребителят се захранва от 80 V батерия с ток 30 A. За нормална работа на потребителя е допустим 3% спад на напрежението в алуминиеви проводници с напречно сечение 16 mm2. Какво е максималното разстояние от батерията до потребителя?

Допустим спад на напрежението в линията U = 3/100 ∙ 80 = 2,4 V.

Съпротивлението на проводниците е ограничено от допустимия спад на напрежението rpr = U / I = 2.4 / 30 = 0.08 Ohm.

Използвайки формулата за определяне на съпротивлението, изчисляваме дължината на проводниците: r = ρ ∙ l / S, откъдето l = (r ∙ S) / ρ = (0,08 ∙ 16) / 0,029 = 44,1 m.

Ако потребителят е на 22 м от батерията, напрежението в нея ще бъде по -малко от 80 V на 3%, т.е. равен на 77,6 V.

7. Телеграфната линия с дължина 20 км е изработена от стоманена тел с диаметър 3,5 мм. Обратната линия се заменя със заземяване чрез метални шини. Съпротивлението на прехода между шината и земята е rz = 50 Ohm. Какво трябва да бъде напрежението на батерията в началото на линията, ако съпротивлението на релето в края на линията е rр = 300 Ohm, а токът на релето е I = 5 mA?

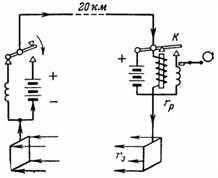
Ориз. 6.

Схемата за свързване е показана на фиг. 6. Когато телеграфният ключ е натиснат на мястото на изпращане на сигнала, релето на приемащото място в края на линията привлича котвата К, която от своя страна включва бобината на записващия апарат със своя контакт. Изходното напрежение трябва да компенсира спада на напрежението в линията, приемното реле и преходните съпротивления на заземяващите шини: U = I ∙ rl + I ∙ rр + I ∙ 2 ∙ rз; U = I ∙ (rл + rр + 2 ∙ rз).

Напрежението на източника е равно на произведението на тока и общото съпротивление на веригата.

Напречно сечение на проводника S = (π ∙ d ^ 2) / 4 = (π ∙ 3,5 ^ 2) / 4 = 9,6 mm2.

Линейно съпротивление rl = ρ ∙ l / S = 0,11 ∙ 20 000 / 9,6 = 229,2 ома.

Резултатно съпротивление r = 229.2 + 300 + 2 ∙ 50 = 629.2 Ohm.

Изходно напрежение U = I ∙ r = 0,005 ∙ 629,2 = 3,146 V; U≈3.2 V.

Спадът на напрежението в линията по време на преминаване на ток I = 0,005 A ще бъде: Ul = I ∙ rl = 0,005 ∙ 229,2 = 1,146 V.

Относително ниският спад на напрежението в линията се постига поради ниската стойност на тока (5 mA). Следователно, в приемната точка трябва да има чувствително реле (усилвател), което се включва от слаб 5 mA импулс и чрез неговия контакт включва друго, по -мощно реле.

8. Колко високо е напрежението на лампите във веригата на фиг. 28, когато: а) двигателят не е включен; б) двигателят стартира; в) двигателят работи.

Двигателят и 20 лампи са свързани към мрежово захранване 110 V. Лампите са проектирани за 110 V и 40 W. Пусковият ток на двигателя е Ip = 50 A, а номиналният му ток е In = 30 A.

Въведената медна жица има напречно сечение 16 mm2 и дължина 40 m.

Фиг. 7 и условията на проблема, може да се види, че токът на двигателя и лампите причинява спад на напрежението в линията, следователно напрежението в товара ще бъде по -малко от 110 V.

Ориз. 7.

U = 2 ∙ Ul + Ulamp.

Следователно напрежението върху лампите Ulamp = U-2 ∙ Ul.

Необходимо е да се определи спада на напрежението в линията при различни токове: Ul = I ∙ rl.

Съпротивление на цялата линия

2 ∙ rl = ρ ∙ (2 ∙ l) / S = 0,0178 ∙ (2 ∙ 40) / 16 = 0,089 Ohm.

Токът, преминаващ през всички лампи

20 ∙ Ilamp = 20 ∙ 40/110 = 7,27 A.

Спад на напрежението в мрежата, когато са включени само лампи (без двигател),

2 ∙ Ul = Ilamp ∙ 2 ∙ rl = 7,27 ∙ 0,089 = 0,65 V.

Напрежението в лампите в този случай е:

Ulamp = U-2 ∙ Ul = 110-0,65 = 109,35 V.

При стартиране на двигателя лампите ще светят по -слабо, тъй като спадът на напрежението в линията е по -голям:

2 ∙ Ul = (Ilamp + Idv) ∙ 2 ∙ rl = (7,27 + 50) ∙ 0,089 = 57,27 ∙ 0,089 = 5,1 V.

Минималното напрежение на лампите при стартиране на двигателя ще бъде:

Ulamp = Uc-2, Ul = 110-5,1 = 104,9 V.

Когато двигателят работи, спадът на напрежението в линията е по -малък, отколкото при стартиране на двигателя, но повече, отколкото когато двигателят е изключен:

2 ∙ Ul = (Ilamp + Inom) ∙ 2 ∙ rl = (7,27 + 30) ∙ 0,089 = 37,27 ∙ 0,089 = 3,32 V.

Напрежението на лампите при нормална работа на двигателя е:

Ulamp = 110-3.32 = 106.68 V.

Дори леко намаляване на напрежението на лампите спрямо номиналното значително влияе върху яркостта на осветлението.