Топологии на схеми — основни понятия

Електрическата верига е съвкупност от устройства (елементи) и свързващи ги проводници, през които може да тече електрически ток. Всички елементи на електрическите вериги споделят в пасивни и активни.

Активните елементи преобразуват различни видове енергия (механична, химическа, светлинна и т.н.) в електрическа. При пасивни елементи електрическата енергия се превръща в други видове енергия. Активните елементи се наричат ​​източници, пасивните се наричат ​​потребители или приемници.

В теорията на схемите се разглеждат идеализирани модели на електрически елементи. Това прави описанието на елементите възможно най -просто. По -сложни, реални елементи се моделират от набор от идеализирани елементи.

Основните пасивни елементи на електрическите вериги са резистор (резистивен елемент), индуктор (индуктивен елемент) и кондензатор (капацитивен елемент). Елементи са инсталирани в електрическа верига за генериране на напрежение и ток с дадена стойност и форма (виж — Електрическа верига и нейните елементи).

Електрическата верига се състои от разклонения и възли. Клон — това е участък от електрическа верига (верига), през която протича същия ток. Възел — свързване на три или повече клона. На електрическата диаграма възелът е обозначен с точка (фиг. 1).

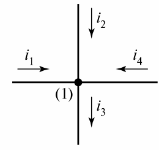
Ориз. 1. Определяне на възела в диаграмата

Ако е необходимо, възлите на диаграмата са номерирани отляво надясно отгоре надолу.

На фиг. 2 показва резистивно-капацитивния клон, в който протича токът iС.

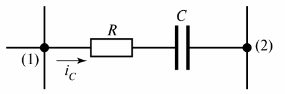
Ориз. 2. Резистивно-капацитивен клон

Може да се даде и друго определение на клон — това е участък от верига между два съседни възела (възли (1) и (2) на фиг. 2).

Верига Има ли някакъв затворен път в електрическата верига. Контурът може да бъде затворен чрез всякакви клони, включително условни клони, чието съпротивление е равно на безкрайността.

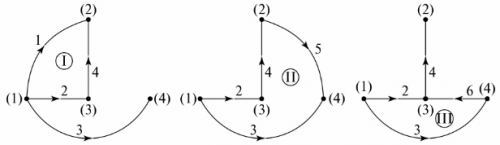
На фиг. 3 показва разклонена електрическа верига, която се състои от три разклонения.

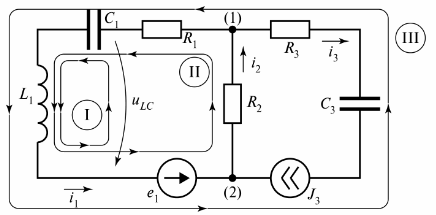
Ориз. 3. Електрическа верига с две вериги

Диаграмата показва три вериги, а верига I се затваря чрез клон с безкрайно съпротивление. Този клон е посочен като напрежение тиLC.

За веригата на фиг. 3 възможно е да се съставят много контури, които са затворени чрез реални или условни разклонения, но за изчисляване на електрическия шум се използва понятието «независим контур». Броят на независимите контури на веригата винаги се определя като минимум, необходим за изчислението.

Независимите вериги винаги са затворени, но клонове, които имат съпротивление, не равно на безкрайността, и всяка независима верига включва поне един клон, който не е включен в други вериги. За сложни електрически вериги можете да определите броя на независимите вериги, като използвате схемата на веригата.

По графика на електрическа верига се извиква условно изображение на веригата, при което всеки клон се заменя с линеен сегмент. Елементите в клоните не се показват. Например, на фиг. 4 показва разклонена електрическа верига и нейната графика.

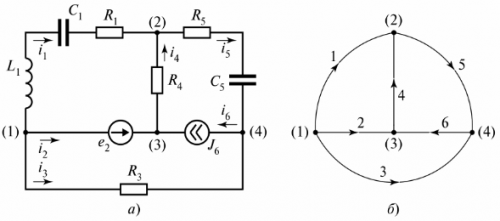
Ориз. 4. Разклонена електрическа верига: а — електрическа схема, б — диаграма

За да съставите диаграма на диаграма, трябва да свържете възлите с линии на разклонение, без да посочвате елементи върху тях. Клоните са номерирани, а посоките на токовете по тях са обозначени със стрелки. Самата графика няма физически смисъл, но може да се използва за определяне на броя и вида на независимите контури. За тази цел се изготвя «графично дърво».

Графично дърво Представлява графика на верига, на която възлите са свързани с клони по такъв начин, че не се получава нито един затворен контур. Може да има няколко опции за показване на графично дърво. На фиг. 5 показва две възможни опции за веригата на фиг. 4.

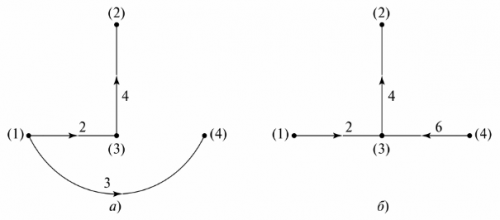
Ориз. 5. Графично дърво на схемата

Броят на липсващите клони в графичното дърво е равен на броя на независимите контури на веригата. В примера това са три клона, три независими контура. Конфигурацията на независими контури може да се получи чрез последователно свързване на възлите на графичното дърво с клони, които не са посочени на графичното дърво. Например, за графично дърво на фиг. 5, а независимите контури са показани на фиг. 6.

Ориз. 6. Определяне на независими контури чрез графичното дърво

Изборът на опция за конфигуриране на независими схеми за изчисляване на веригата се извършва при анализ на веригата. Трябва да изберете такива контури, така че изчислението да е възможно най -просто, т.е. броят на зависимите уравнения в системата е минимален.

Топологичните уравнения установяват връзка между напрежения и токове на верига, а броят и видът на уравненията не зависят от това кои елементи са включени в разклоненията. Топологичните уравнения включват уравнения, съставени според законите на Кирххоф.