Теория на автоматите, крайни автомати
Структурата, дизайнът, принципът на работа на различни машини до голяма степен се определят от функционалното й предназначение. Разграничете технологични, транспортни, изчислителни, военни и други машини. В различни индустрии широко се въвеждат цели автоматични комплекси, предназначени да изпълняват сложни технологични процеси. Автоматите са проектирани и изградени, които изпълняват различни логически функции (логически машини).

Теория на автоматите — раздел кибернетика, възникнали под влияние на изискванията на технологията на цифровите компютри и машини за управление. Дискретни автомати, изучавани в теорията на автоматите, са абстрактни модели на реални системи (както технически, така и биологични), които обработват дискретна (цифрова) информация на дискретни стъпки във времето.
Теорията на автоматите се основава на точни математически концепции, които формализират интуитивни представи за функционирането (поведението) на автомата и за неговата структура (вътрешна структура).
В този случай трансформацията на информация винаги се разбира като операция, която трансформира входните последователности, съставени от букви от входната азбука, в изходни последователности, съставени от букви от изходната азбука.
Апаратът на математическата логика, алгебрата, теорията на вероятностите, комбинаториката и теорията на графите е широко използван.
Проблемът с теорията на автоматите в някои от нейните части (структурна теория на автоматите) нарасна от теорията на релейно-контактните вериги, който започва да се оформя в края на 30 -те години. включващи методи за логическа алгебра.

В структурната теория на автоматите се изследват различни видове схеми, предназначени да опишат как се създава сложен автомат от по -прости компоненти (елементи), правилно свързани в една система.
Друго направление, наречено абстрактна теория на автоматите, изучава поведението на автоматите (тоест естеството на трансформацията на информацията, извършена от тях), като същевременно се абстрахира от спецификата на тяхната вътрешна структура и възниква през 50 -те години на миналия век.
В рамките на абстрактната теория на автоматите съдържанието на понятията „автомат“ и „машина“ по същество се изчерпва от стандартното описание на трансформацията на информация, която се извършва от автомат. Подобна трансформация може да бъде детерминистична, но може да има и вероятностен характер.
Най -изучавани са детерминираните машини (автомати), които включват крайни автомати — основният обект на изследване в теорията на автоматите.
Машината с крайни състояния се характеризира с ограничено количество памет (броя на вътрешните състояния) и се определя с помощта на преходна функция. С известна разумна идеализация всички съвременни математически машини и дори мозъкът, от гледна точка на тяхното функциониране, могат да се разглеждат като крайни автомати.
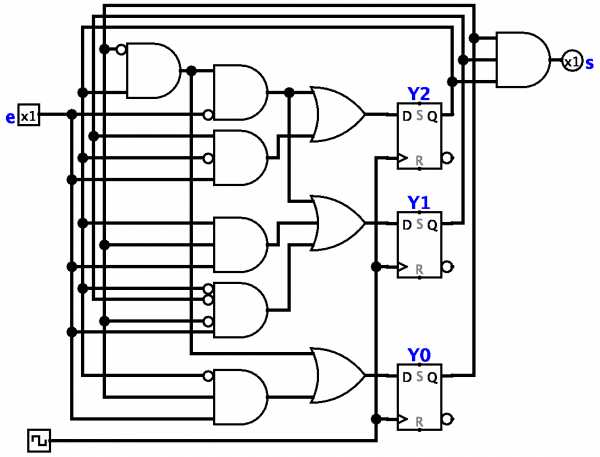
Термините „последователна машина“, „автомат Мили“, „автомат Мур“ се използват в литературата (а не еднакво от всички автори) като синоними на термина „краен автомат“ или за подчертаване на определени характеристики във функциите на преход на краен автомат.
Автомати с неограничена памет е машина на Тюринг, способна да извършва (потенциално) всяка ефективна трансформация на информация. Понятието „машина на Тюринг“ възниква по -рано от понятието „машина с крайни състояния“ и се изучава главно в теорията на алгоритмите.
Абстрактната теория на автоматите е тясно свързана с добре известни алгебрични теории, например теорията на полугрупите. От приложна гледна точка интерес представляват резултатите, характеризиращи трансформацията на информацията в автомат по отношение на размера на паметта.
Такъв е случаят например при проблеми с експерименти върху автомати (произведения на Е.Ф. Мур и др.), При които от резултатите от експериментите се получава една или друга информация за преходните функции на автомата или за капацитета на паметта му .
Друга задача е да се изчислят периодите на изходните последователности, въз основа на наличната информация за размера на паметта на автомата и периодите на входните последователности.
От голямо значение е разработването на методи за минимизиране на паметта на крайни автомати и изучаването на тяхното поведение в случайни среди.
В абстрактната теория на автоматите проблемът за синтеза е следният. По отношение на някакъв ясно формализиран език, условията са написани за поведението на проектирания автомат (за събитието, представено в автомата). В този случай е необходимо да се разработят методи, които според всяко писмено условие:
1) разберете дали съществува такъв краен автомат, че трансформираната от него информация отговаря на това условие;
2) ако да, тогава се изграждат преходните функции на такъв краен автомат или се оценява неговият размер на паметта.
Решението на задачата за синтез в такава формулировка предполага предварително създаване на удобен език за записване на условията на работа на автомат с удобни алгоритми за преход от записващи към преходни функции.
В структурната теория на автоматите синтезният проблем се състои в изграждането на верига от елементи от даден тип, която реализира краен автомат, даден от неговите преходни функции. В този случай те обикновено излагат някакъв критерий за оптималност (например минималния брой елементи) и се стремят да получат оптимална схема.
Както се оказа по-късно, това означава, че някои от методите и концепциите, разработени по-рано по отношение на релейно-контактните схеми, са приложими за вериги от друг тип.
Във връзка с развитието на електронните технологии най -широко разпространени са схемите от функционални елементи (логически мрежи). Специален случай на логически мрежи са абстрактните невронни мрежи, чиито елементи се наричат неврони.
Разработени са много методи за синтез, в зависимост от типа на схемите и от трансформацията на информация, за чието изпълнение са предназначени (Синтез на релейни устройства).
Вижте —Минимизиране на комбинационни схеми, карти на Карно, синтез на вериги
Машина с крайно състояние — математически модел на система за управление с фиксиран (неспособен да се увеличава по време на работа) размер на паметта.
Концепцията за краен автомат е математическа абстракция, която характеризира общите характеристики на набор от системи за управление (например многоциклово релейно устройство). Всички такива системи имат общи черти, които са естествени за приемане като дефиниция на краен автомат.
Всеки завършен автомат има вход, изложен на външни влияния и вътрешни елементи. Както за входните, така и за вътрешните елементи има фиксиран брой дискретни състояния, които те могат да приемат.
Промяната в състоянията на входните и вътрешните елементи се случва в дискретни моменти от времето, интервалите между които се наричат кърлежи. Вътрешното състояние (състоянието на вътрешните елементи) в края на лентата се определя изцяло от вътрешното състояние и състоянието на входа в началото на лентата.
Всички други определения на краен автомат могат да бъдат сведени до тази характеристика, по -специално дефиниции, които приемат, че краен автомат има изход, който зависи от вътрешното състояние на автомата в даден момент.
От гледна точка на такава характеристика, естеството на нейните входове и вътрешните състояния няма значение за описанието на завършен автомат. Вместо входове и състояния, можете просто да разгледате техните номера в произволно избрана номерация.
Машината на състоянието ще бъде зададена, ако е посочена зависимостта на номера на нейното вътрешно състояние от номера на предишното вътрешно състояние и номера на предишното състояние на входа. Такава задача може да бъде под формата на финална маса.
Друг често срещан начин за дефиниране на завършен автомат е изграждането на т.нар. преходни диаграми. Входните състояния често се наричат просто входове, а вътрешните състояния са просто състояния.
Машината с крайно състояние може да бъде модел както на технически устройства, така и на някои биологични системи. Автомати от първия тип са например релейни устройства и различни електронни компютри, вкл. програмируеми логически контролери.
В случай на релейно устройство, ролята на входните състояния се играе от комбинации от състояния на чувствителните елементи на релейното устройство (всяка комбинация от такива състояния е «сложно състояние», характеризиращо се с индикация за всички чувствителни елементи на тези дискретни заявява, че имат в даден момент). По същия начин комбинациите от състояния на междинни елементи на релейно устройство играят ролята на вътрешни състояния.

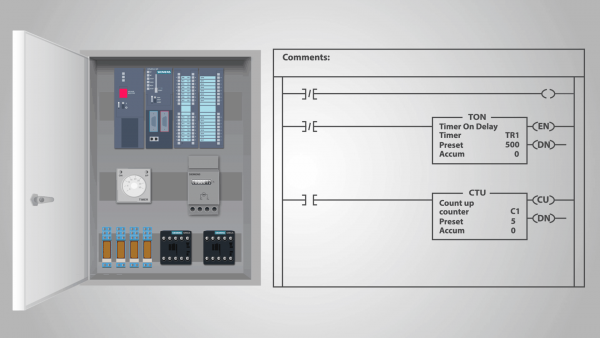
Програмируем логически контролер (PLC) е пример за устройство за релейно действие, което може да се нарече самостоятелна машина на състоянието.
Всъщност, след като програмата е била въведена в PLC и контролерът е започнал да изчислява, тя не е изложена на външни влияния и всяко следващо състояние се определя изцяло от предишното си състояние. Можем да приемем, че входът има едно и също състояние във всеки тактов цикъл.
Обратно, всеки краен автомат, който има единственото възможно състояние на вход, естествено се нарича автономен, тъй като в този случай външната среда не носи информация, която контролира поведението му.
Вижте също:
Използването на микропроцесорни системи в електротехниката на примера за използване на PLC
