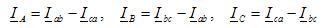Изчисляване на трифазни вериги

Верига трифазен променлив ток се състои от трифазно захранване, трифазен потребител и проводниците на комуникационната линия между тях.

Симетрично трифазно захранване може да бъде представено като три еднофазни захранвания, работещи на една и съща честота със същото напрежение и с ъгъл на фаза във времето 120 °. Тези източници могат да бъдат свързани чрез звезда или триъгълник.

Когато са свързани със звезда, условното начало на фазите се използва за свързване на три линейни проводника A, B, C, а краищата на фазите се обединяват в една точка, наречена неутрална точка на източника на захранване (трифазен генератор или трансформатор). Към тази точка може да бъде свързан неутрален проводник N. Схемата за свързване на звездата на източника на захранване е показана на Фигура 1, а.

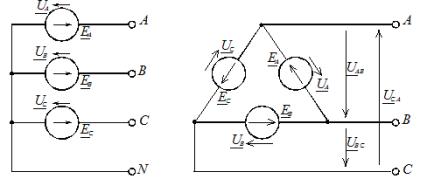
Ориз. 1. Схеми на свързване на фазите на захранването: а — от звезда; b — триъгълник

Напрежението между линейния и неутралния проводник се нарича фаза, а между линейните проводници — линия (за повече подробности вижте тук — Линейно и фазово напрежение).

V интегрирана форма записите на изразите за фазовите напрежения са:

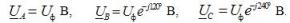
Съответните напрежения на линията, когато са свързани със звезда:

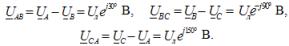
Тук Uf е модулът на фазовото напрежение на източника на захранване, а Ul е модулът на линейното напрежение. В симетрична трифазна система, когато фазите на източника са свързани със звезда, има връзка между тези напрежения:

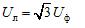
Когато фазите са включени с триъгълник, фазовите захранвания са свързани последователно в затворен контур (Фигура 1, б).

Три линейни проводника A, B, C се извеждат от точките на комбиниране на източниците помежду си, отивайки към товара. От фигура 1, б може да се види, че изходите на фазовите източници са свързани към линейни проводници и следователно, когато фазите на източника са свързани с триъгълник, фазовите напрежения са равни на линейни. В този случай няма неутрален проводник.

Товар може да бъде свързан към трифазно захранване. По отношение на размера и естеството, трифазният товар може да бъде симетричен и асиметричен.

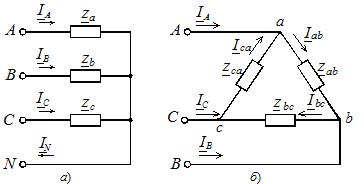
В случай на симетрично натоварване, сложните съпротивления на трите фази са еднакви, а ако тези съпротивления са различни, тогава натоварването е небалансирано. Фазите на натоварване могат да бъдат свързани помежду си със звезда или триъгълник (Фигура 2), независимо от схемата на свързване на източника.

Ориз. 2. Схеми на свързване на фазите на натоварване

Звездната връзка може да бъде със или без неутрален проводник (виж Фигура 2, а). Отсъствието на неутрален проводник елиминира твърдото свързване на напрежението на натоварването към захранващото напрежение, а в случай на асиметрично фазово натоварване, тези напрежения не са равни помежду си. За да ги разграничим, се съгласихме да използваме главни букви в индексите на буквените обозначения на напреженията и токовете на захранването и малки букви в параметрите, присъщи на товара.

Алгоритъмът за анализ на трифазна верига зависи от схемата на свързване на товара, първоначалните параметри и целта на изчислението.

За определяне на фазовите напрежения с небалансиран товар, свързан със звезда без неутрален проводник, се използва методът с два възела. Според този метод изчислението започва с определяне на напрежението UN между неутралните точки на захранването и товара, наречено напрежение на неутрално отклонение:

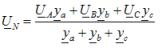
където ya, yb, yc — допустими стойности на съответните фази на натоварването в сложна форма

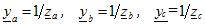
Напреженията върху фазите на небалансиран товар се намират от изразите:

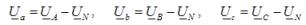
В специалния случай на дисбаланс на товара, когато при липса на неутрален проводник възникне късо съединение в една от фазите на натоварване, напрежението на неутралното отклонение е равно на фазовото напрежение на захранването на фазата, в която късото възникна верига.

Напрежението на затворената фаза на товара е нула, а на другите две е числено равно на линейното напрежение. Да предположим например, че късо съединение възниква във фаза В. Неутралното напрежение на отклонение за този случай е UN = UB. Тогава фазовите напрежения върху товара:

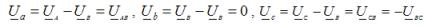
Фазови токове в товара, те също са токове на линейни проводници за всякакъв вид натоварване:

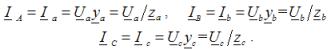
В задачите при изчисляване на трифазни вериги се разглеждат три варианта за свързване на трифазни консуматори със звезда: свързване към неутрален проводник в присъствието на потребители в три фази, свързване към неутрален проводник при липса на консуматори в една от фазите и връзка без неутрален проводник с късо съединение в една от фазите на натоварване …

В първата и втората версия съответните фазови напрежения на захранването се намират върху фазите на натоварване и фазовите токове в товара се определят по горните формули.

В третата версия напрежението на фазите на натоварване не е равно на фазовото напрежение на захранването и се определя с помощта на зависимостите

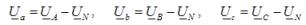
Токовете в две несъкратени фази се определят съгласно закона на Ом, като част от разделянето на фазовото напрежение на импеданса на съответната фаза. Токът на късо съединение се определя с помощта на уравнение, базирано на първият закон на Кирххофсъставен за неутралната точка на товара.

За горния пример за късо съединение във фаза В:

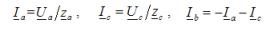
За всеки тип натоварване трифазните активни и реактивни мощности са равни съответно на сумата от активната и реактивната мощност на отделните фази. За да определите тези фазови мощности, можете да използвате израза

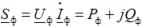
където Uf,Азf, е комплексът на напрежението и комплексът от спрегнати токове във фазата на натоварване; Pf, Qf — активна и реактивна мощност във фазата на натоварване.

Трифазна активна мощност: P = Pа + Pb + Pс

Трифазна реактивна мощност: Q = Qа + Qb + Вс

Трифазна привидна мощност:

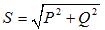
Когато потребителите са свързани с триъгълник, веригата придобива формата, показана на фигура 2, б. В този режим фазовото свързване на симетричното захранване е без значение.

На фазите на натоварване се откриват напрежения между линиите на захранването. Фазовите токове в товара се определят с помощта Законът на Ом за участък от веригаАзf = Uf /zf, където Uf — фазово напрежение в товара (съответстващо на мрежовото напрежение на източника на захранване); zf е общото съпротивление на съответната фаза на товара.

Токовете в линейни проводници се определят чрез фазови такива въз основа на първия закон на Кирххоф за всеки възел (точки a, b, c) на веригата, показана на фигура 2, b: