Изчисляване на капацитета на кондензатора

Капацитет C е способността на кондензатора да приема (съхранява и задържа) количеството електричество Q в амперсекунди или заряда Q във висулките. Ако кажете на някое тяло, например топка, електрически заряд (количество електричество) Q, тогава електроскоп, свързан между това тяло и земята, ще покаже напрежение U (фиг. 1). Това напрежение е пропорционално на заряда и също зависи от формата и размера на тялото.

Връзката между заряд Q и напрежение U се изразява с формулата Q = C ∙ U.

Константата на пропорционалност C се нарича капацитет на тялото. Ако тялото има формата на топка, капацитетът на тялото е пропорционален на радиуса на топката r.

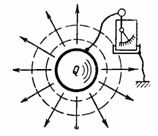
Ориз. 1.

Мерната единица за капацитет е фарад (F).

Тялото има капацитет 1 F, когато с заряд 1 k се получи напрежение от 1 V. между него и земята. Фарадите са много голяма мерна единица и затова на практика се използват по -малки единици: микрофарада (μF), нанофарада (nF) и пикофарада (pF) …

Тези единици са свързани със следните съотношения: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Капацитетът на топката с радиус 1 cm е 1,1 pF.

Не само изолирано тяло може да натрупа заряд, но и специално устройство, наречено кондензатор. Кондензаторът се състои от две или повече плочи (плочи), които са разделени от диелектрик (изолация).

На фиг. 2 показва схема с източник на постоянен ток, свързан към кондензатор. При включване се образува положителен заряд + Q в дясната плоча на кондензатора и отрицателен заряд –Q в лявата плоча. По време на заряд на кондензатора през веригата протича ток, който спира след края на зареждането; тогава напрежението в кондензатора ще бъде равно на e. и т.н. с. източник U. Зарядът на плочата на кондензатора, напрежението и капацитетът са свързани със съотношението Q = C ∙ U. В този случай в диелектрика на кондензатора се образува електростатично поле.

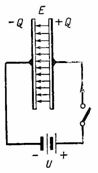
Ориз. 2.

Капацитетът на кондензатор с въздушен диелектрик може да се изчисли по формулата C = S / (4 ∙ π ∙ d) ∙ 1.11, pF, където S е площта на една плоча, cm2; d е разстоянието между плочите, cm; C е капацитетът на кондензатора, pF.

Капацитетът на кондензатор, състоящ се от n пластини (фиг. 3), е равен на: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

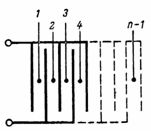
Ориз. 3.

Ако пространството между плочите се запълни с друг диелектрик, например хартия, капацитетът на кондензатора ще се увеличи с коефициент ε. Когато се използва хартиена изолация, капацитетът ще се увеличи 3 пъти, с изолация от слюда — 5-8 пъти, със стъкло — 7 пъти и т.н. Стойността на ε се нарича диелектрична константа на диелектрика.

Общата формула за определяне на капацитета на кондензатор с диелектрична константа ε (epsilon) е: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Тази формула е полезна за изчисляване на малки променливи кондензатори за радиостанции. Същата формула може да бъде представена като: C = (ε_0 ∙ ε ∙ S) / d, където ε_0 е диелектричната константа или диелектричната константа на вакуума (ε_0 = 8.859 ∙ 10 ^ (- 12) F / m); ε е диелектричната константа на диелектрика.

В тази формула размерите се заменят в метри, а капацитетът се получава във фаради.

Примери за

1. Какъв капацитет има планетата Земя, чийто радиус е r = 6378 км?

Тъй като капацитетът на сфера с радиус 1 cm е равен на 1,11 pF, капацитетът на Земята е: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Капацитетът на една топка, равен по размер на нашата планета, е относително малък. Електролитните кондензатори с малък размер имат такъв капацитет).

2. Определете капацитета на кондензатор, състоящ се от две пластини, всяка от които има площ S = 120 cm2.

Плочите са разделени от слой въздух с дебелина d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21,20 pF .. .

3.Определете капацитета на кондензатора с данните, посочени в предишния пример, ако пространството между плочите е запълнено с восъчна хартия с диелектрична константа ε = 4, стъкло (ε = 7), електрически картон (ε = 2), слюда (ε = 8).

Кондензатор с восъчна хартия има капацитет C = ε ∙ (S ∙ 1.11) / (4 ∙ π ∙ d) = 4 ∙ 21.2 = 84.8 pF.

Капацитетът на кондензатор със стъкло е C = 7 ∙ 21.2 = 148.4 pF.

Капацитетът на кондензатора с картон е C = 2 ∙ 21.2 = 42.3 pF.

Капацитетът на кондензатора със слюда е C = 8 ∙ 21.2 = 169.6 pF.

4. Какъв е капацитетът на въздушен ротационен кондензатор за радиоприемник, състоящ се от 20 плочи с площ 20 cm2, ако разстоянието между пластините е 0,06 cm (фиг. 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Кондензаторът, показан на фиг. 3, се състои от отделни най-прости кондензатори с две пластини, чийто брой е равен на n-1.

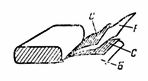
5. Хартиен кондензатор с капацитет C = 2 μF се състои от две ленти от станиол C и две ленти от диелектрик, направен от восъчна хартия B с диелектрична константа ε = 6. Дебелината на восъчната хартия е d = 0,1 мм. Сгънатите ленти се навиват, изводите се правят от стоманените плочи. Определете дължината на кондензаторната стоманена лента, ако нейната ширина е 4 cm (фиг. 4).

Ориз. 4.

Първо, ние определяме площта на една лента по формулата C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, откъдето S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = (2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Дължината на всяка лента е l = 37680/4 = 9420 cm = 94,2 m.